Расстояние от точки до прямой на плоскости
Будем предполагать, что прямая l задананормальным уравнением A×x + B×y + C = 0, где A2 + B2 = 1 в декартовой системе координат.
На плоскости задана произвольная точка P(x0 ; y0) и нужно найти расстояние d(P, l) от неё до прямой l. Если провести через т. P прямую l¢ || l, то искомое расстояние будет равно d(P, l) = HH¢, где OH¢ ^ l¢, OH ^ l.
 Переходим к вычислениям. Направляющие векторы прямых l и l¢ совпадают, поэтому уравнение прямой l¢ записывается в нормальном виде A×x+B×y+C¢ = 0, где C¢ находится из условия прохождения l¢ через точку P : A×x0+B×y0+C¢ = 0, т.е. выполнено равенство C¢ = –(A×x0+B×y0 ) .
Переходим к вычислениям. Направляющие векторы прямых l и l¢ совпадают, поэтому уравнение прямой l¢ записывается в нормальном виде A×x+B×y+C¢ = 0, где C¢ находится из условия прохождения l¢ через точку P : A×x0+B×y0+C¢ = 0, т.е. выполнено равенство C¢ = –(A×x0+B×y0 ) .
При этом, H¢(–A×C¢; –B×C¢), H(–A×C; –B×C), 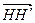 (–A×(C¢–C); –B×(C¢–C)) и HH¢ = |
(–A×(C¢–C); –B×(C¢–C)) и HH¢ = | 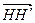 | =
| = 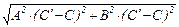 =
= 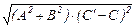 = |C¢ – C| = |–(A×x0+B×y0)–C| = = |A×x0+B×y0+C| .
= |C¢ – C| = |–(A×x0+B×y0)–C| = = |A×x0+B×y0+C| .
Одновременно получена формула для расстояния d(l, l¢) между параллельными прямыми, заданными нормальными уравнениями A×x+B×y+C = 0 и A×x+B×y+C¢ = 0 : d(l, l¢) = = |C¢ – C| .
Как изменятся формулы, если прямая задана общим уравнением A×x+B×y+C = 0 в декартовых координатах ? Нормальное уравнение получается умножением общего уравнения на множитель 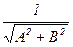 . Следовательно, все формулы умножатся на этот множитель: d(P, l) =
. Следовательно, все формулы умножатся на этот множитель: d(P, l) = 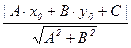 , d(O, l) =
, d(O, l) = 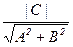 , d(l, l¢) =
, d(l, l¢) = 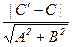 .
.
Подытожим все выводы в теореме:
Теорема (о расстояниях от точки до прямой и между прямыми). Пусть на плоскости даны прямая l с общим уравнением в некоторой декартовой системе координат A×x+B×y+C = 0 (A2+B2 ¹ 0) и точка P(x0 ; y0 ). Тогда d(P, l) = 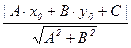 ; в частности, если Р является началом координат О, то d(О, l) =
; в частности, если Р является началом координат О, то d(О, l) = 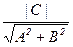 .
.
Если уравнением A×x+B×y+C¢ = 0 задана вторая прямая l¢, параллельная l, то d(l, l¢) = 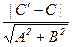 .
.
Дата добавления: 2021-12-14; просмотров: 561;











