Угол между двумя плоскостями
 Пусть в пространстве задана декартова система координат. Рассмотрим две плоскости p1 , p2 с общими уравнениями Аi×x+Bi×y+Ci×z+Di = 0 (Ai2+Bi2+Ci2 ¹ 0, i = 1, 2). Эти плоскости либо совпадают, либо параллельны, либо пересекаются по прямой. В первых двух случаях величина угла между ними считается равной нулю. В третьем случае при пересечении плоскостей образуются четыре двугранных угла (см. рис.), они попарно вертикальные, и величина меньшего из них называется углом между плоскостями p1 и p2 .
Пусть в пространстве задана декартова система координат. Рассмотрим две плоскости p1 , p2 с общими уравнениями Аi×x+Bi×y+Ci×z+Di = 0 (Ai2+Bi2+Ci2 ¹ 0, i = 1, 2). Эти плоскости либо совпадают, либо параллельны, либо пересекаются по прямой. В первых двух случаях величина угла между ними считается равной нулю. В третьем случае при пересечении плоскостей образуются четыре двугранных угла (см. рис.), они попарно вертикальные, и величина меньшего из них называется углом между плоскостями p1 и p2 .
Как вычислять угол между плоскостями ? Рассмотрим прямую l пересечения плоскостей p1 и p2 с направляющим вектором a(a ; b ; g) и произвольной точкой P(x0 ; y0 ; z0) Î l. Тогда величина угла Ð (p1 , p2) = j равна углу Ð (k1 , k2) между двумя прямыми k1 и k2, перпендикулярными прямой l и проходящими через т. P в плоскостях pi (i = 1, 2). Как было отмечено при выводе нормального уравнения плоскости, для любой плоскости с общим уравнением A×x+B×y+C×z+D = 0 вектор N(A; B; C) перпендикулярен этой плоскости (т.е. перпендикулярен любому направленному отрезку с концами в этой плоскости).Поэтому для плоскости s,проходящей через прямые k1 , k2 в качестве вектора N можно взять направляющий вектор a прямой l, перпендикулярный обеим прямым k1 и k2 .Таким образом, s имеет общее уравнениевида a×x+b×y+g×z+D = 0, где D = –a×x0–b×y0–g×z0 получается из условия P(x0 ; y0 ; z0) Î s.
С другой стороны, векторы Ni(Ai ; Bi ; Ci), перпендикулярны плоскостям pi (i = 1, 2), а значит и прямой l. Поэтому плоскость с направляющими векторами N1, N2 и проходящая через т. P совпадает с s. Кроме того, из условий N1 ^ k1 , N2 ^ k2 следует, что углы Ð (k1 , k2) и Ð (N1 , N2) с общей вершиной P в плоскости s имеют соответственно перпендикулярные стороны. Значит либо j = Ð (k1 , k2) = Ð (N1 , N2) и cos j = cos Ð (N1 , N2), либо j = Ð (k1 , k2) = p – Ð (N1 , N2) и cos j = – cos Ð (N1 , N2). В любом случае cos j = = |cos Ð (N1 , N2)| . Таким образом, получены формулы:

Эти формулы справедливы и в случае коллинеарных векторов N1 , N2 , т.е. когда плоскости p1 и p2 совпадают или параллельны. Особенно просто вычисляется угол между плоскостями, заданными нормальными уравнениями Аi×x+Bi×y+Ci×z+Di = 0 (Ai2+Bi2+Ci2 = 1, i = 1, 2): Ð (p1 , p2) = arc cos |A1×A2+B1×B2+C1×C2 |.
Следствие (о перпендикулярности плоскостей).Плоскости p1 и p2 , заданные в некоторой декартовой системе координат общими уравнениями Аi×x+Bi×y+Ci×z+Di = 0 (Ai2+Bi2+Ci2 ¹ 0), i = 1, 2, перпендикулярны (т.е. Ð (p1 , p2) = 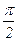 ) тогда и только тогда, когда A1×A2+B1×B2+C1×C2 = 0.
) тогда и только тогда, когда A1×A2+B1×B2+C1×C2 = 0.
Двугранный угол — пространственная геометрическая фигура, образованная двумя полуплоскостями, исходящими из одной прямой, а также часть пространства, ограниченная этими полуплоскостями.
Полуплоскости называются гранями двугранного угла, а их общая прямая — ребром.
Двугранные углы измеряются линейным углом, то есть углом, образованным пересечением двугранного угла с плоскостью, перпендикулярной к его ребру.
У всякого многогранника, правильного или неправильного, выпуклого или вогнутого, есть двугранный угол на каждом ребре.
 Расстояние от точки до плоскости. Пусть задана точка M(u; v; w)Î E3и плоскость p с нормальным уравнением A×x+B×y+C×z+D = 0 (A2+B2+C2= 1). Тогда расстояние r(M, p) от точки M до плоскости p – это min{ MX | X Î p}, и из рисунка видно, что этот минимум достигается при X = Mp (в прямоугольном треугольнике катет короче гипотенузы). Таким образом, r(M, p) = MMp – расстоянию от точки до её проекции на плоскость p. Для нахождения этого расстояния воспользуемся результатами вычислений, проведённых при решении задачи § 8. Имеем
Расстояние от точки до плоскости. Пусть задана точка M(u; v; w)Î E3и плоскость p с нормальным уравнением A×x+B×y+C×z+D = 0 (A2+B2+C2= 1). Тогда расстояние r(M, p) от точки M до плоскости p – это min{ MX | X Î p}, и из рисунка видно, что этот минимум достигается при X = Mp (в прямоугольном треугольнике катет короче гипотенузы). Таким образом, r(M, p) = MMp – расстоянию от точки до её проекции на плоскость p. Для нахождения этого расстояния воспользуемся результатами вычислений, проведённых при решении задачи § 8. Имеем
Mp((1–A2)×u–A×B×v–A×C×w–A×D; –A×B×u+(1–B2)×v–B×C×w–B×D; –A×C×u–B×C×v+(1–C2)×w–C×D).
Поэтому r(M, p) = MMp = 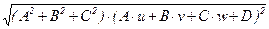 =
= 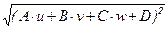 = = |A×u+B×v+C×w+D| .
= = |A×u+B×v+C×w+D| .
В общем случае, когда плоскость задана не нормальным, а общим уравнением, для перехода к нормальному уравнению нужно поделить все коэффициенты общего уравнения на 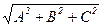 . Таким образом, получится формула r(M, p) =
. Таким образом, получится формула r(M, p) = 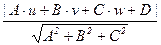 .
.
Дата добавления: 2021-12-14; просмотров: 532;











