Теоремы Эйлера и Ферма

Теорема 10. 2 (теорема Эйлера).Для любого целого числа a, взаимно простого с натуральным модулем m, выполняется сравнение

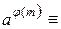1(mod m) .

Доказательство. Пусть r₁, …, r_k – какая-нибудь приведенная система вычетов по модулю m. Тогда k = (m). Согласно свойства приведенной системы множество чисел аr₁, …, аr_k также составляет приведенную систему вычетов. Это значит, что каждое число второй системы лежит в одном классе с каким-либо единственным числом первой системы вычетов. Поэтому справедливы сравнения

аr₁∙ …· аr_k 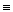r₁ · …∙ r_k (mod m) (1)

Так как каждое из чисел r_j взаимно просто с модулем, то сравнение (1) можно сократить на каждое из чисел r_j. В результате получаем сравнение а^k 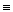1(mod m) или 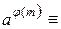1(mod m).

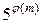
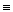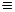Пример.а = 5, m = 9. (5, 9) = 1 1(mod9), т.к. (9) = (3²) = = 3 · (3 – 1) = 6. Итак, 5⁶ 1(mod9).

Рассмотрим частный случай теоремы Эйлера, в котором m = p есть простое число. Тогда (p) = p – 1 и получается следующее утверждение.

Теорема 10.3 (малая теорема Ферма).Если целое число а не делится на простое число p, то

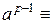1(mod p).

Теорема 10.4 (следствие малой теоремы Ферма).Для любого простого числа p и целого a выполняется сравнение

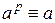(mod p).

Доказательство следует из малой теоремы Ферма:

a ^p – a º a× (a ^p–1 – 1) º 0(mod p)как для целого числа a, делящегося на p, так и для целого числа а взаимно простого с p.

Рассмотрим теперь некоторые применения доказанных теорем. Примеры: 1.Найти остаток от деления 5²⁴⁷на 7.

Так как (5, 7) = 1, то по теореме Эйлера, 5^j(7)º 1 (mod 7)или 5⁶ º 1(mod 7), поскольку (7) = 6. Значит, 5²⁴⁷= (5⁶)⁴¹ × 5 º 1⁴¹ × 5 º 5 (mod 7). Итак, искомый остаток равен 5.

2. Определим последние три цифры в десятичной записи числа 3²⁰⁰⁷. Для этого достаточно сосчитать остаток от деления 3²⁰⁰⁷ на 1000. Так как (1000) = (8) · (125) = 4 · 100 = 400 и (3, 1000) = 1, то по теореме Эйлера выполняется сравнение 3⁴⁰⁰ º 1 (mod 1000). Отсюда следует

3²⁰⁰⁷ = (3⁴⁰⁰)⁵ ·3⁷ º 3⁷ (mod 1000).

Это сравнение означает, что 3²⁰⁰⁷ и 3⁷ = 2187 имеют одинаковые три последние цифры, и десятичная запись числа 3²⁰⁰⁷ оканчивается цифрами 187.

Признаки делимости

Признаки делимости служат для того, чтобы при их помощи можно было определить делимость данного числа n на заданное число d, не выполняя деления. Признаки делимости, естественно, должны быть достаточно простыми, чтобы можно было определить делимость сравнительно быстро.

В школьном курсе рассматривались лишь простейшие из них: признаки делимости на 2, 3, 5, 9, 10. Другие признаки лежат за пределами школьного курса.

Рассмотрим признаки делимости целых чисел, записанных в десятичной системе счисления на 3, 9, 11.

Пусть а_k, a_k-1, …, а₁, а₀ – цифры десятичной записи натурального числа n = ).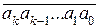

Теорема 10.5 (признаки делимости на 3 и 9).Натуральное число n, записанное в десятичной системе счисления, делится на d такое, что d {3, 9} тогда и только тогда, когда сумма цифр числа n делится на d.

Доказательство. Заметим, что 10¹ º 1 (mod d), 10² º 1 (mod d), … ,

10^k º 1 (mod d). Тогда, используя свойства сравнений, получим:

n = a_k · 10^k + a_k-1 · 10^k-1 + … + а₁ · 10 + а₀ º a_k + a_k-1 + … + а₁ + а₀ (mod d)

Теорема 10.6 (признак делимости на 11).Натуральное число n, записанное в десятичной системе счисления, делится на 11 тогда и только тогда, когда знакочередующаяся сумма цифр числа n делится на 11 т.е.

n = (a_k · 10^k + a_k-1 · 10^k-1 +…+ а₁ · 10 + а₀) 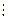11 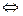(а₀ – а₁ + а₂ – …+ (–1)^k · a_k) 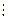11

Доказательство. Заметим, что 10¹ º -1 (mod 11), 10² º 1 (mod 11), … ,

10^k º (-1)^k (mod 11). Тогда, используя свойства сравнений, получим:

n = a_k · (-1)^k + a_k-1 · (-1)^k-1 + … + а₁ · (-1) + а₀ º a₀ – a₁ +…+ (–1)^k · a_k (mod 11)

Примеры:1)2457 делится на 3 и на 9,т.к. 2 + 4 + 5 + 7=18 делится и на 3 и на 9.

2) 234712 не делится на 11, т.к. 2 – 1 + 7 – 4 + 3 – 2 = 5, а 5 не делится на 11.

3) 2132438 делится на 11, т.к. 8 – 3 + 4 – 2 + 3 – 1 + 2 = 11 делится на 11.