ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ЭЙЛЕРА ДВИЖЕНИЯ НЕВЯЗКОЙ ЖИДКОСТИ

Дифференциальные уравнения равновесия Эйлера дают возможность установить напряженное состояние неподвижной жидкости. Для движущейся жидкости необходимо получить связь действующих на нее сил не только с напряжениями, но и со скоростями. В теоретической механике известен способ использования уравнений статики для описания движения тел – принцип Даламбера. В соответствии с ним в исходные уравнения равновесия нужно ввести силы инерции.

.

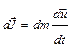Все величины в уравнениях отнесены к массе жидкой частицы и имеют размерность ускорения. Поэтому и сила инерции должна быть также отнесена к массе частицы. Тогда она численно равно ускорению движения:

.

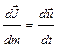Проекции удельной силы инерции на соответствующие оси выражаются через компоненты скорости следующим образом:

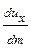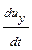; и .

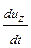Согласно принципу Даламбера, уравнения движения получают вид:

;

;

.

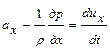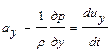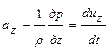Эти уравнения справедливы для невязкой жидкости, так как при выводе исходных зависимостей не были учтены касательные напряжения.