Теорема 10.7 (общий признак делимости Паскаля).
Для того, чтобы число n, записанное в произвольной q – ичной системе счисления в виде: n = ak qk + ak-1 qk-1 + …+ a1 q + a0 делилось на m, где 1 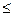 ak
ak 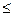 q-1, 0
q-1, 0 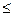 ai
ai 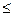 q-1, i
q-1, i  {0, 1, … , n} необходимо и достаточно, чтобы число Q = ak rk + ak-1 rk-1 + …+ a1 r1 + a0 r0 делилось на m.
{0, 1, … , n} необходимо и достаточно, чтобы число Q = ak rk + ak-1 rk-1 + …+ a1 r1 + a0 r0 делилось на m.
(аk, ak-1, …, а1, а0 – цифры q - ичной записи натурального числа n = 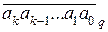 , а ri – наименьшие по абсолютной величине вычеты степеней qi при i
, а ri – наименьшие по абсолютной величине вычеты степеней qi при i  {0, 1,…, n}).
{0, 1,…, n}).
МЕТОДИКА 20.
Учебник математики 6кл. Н. Веленкин и др.
1. Основные математические понятия: четные и нечетные числа
2. Основные предложения темы: признаки делимости натурального числа на 2, 3, 5, 10.
3. Ранее изученный материал: натуральное число, деление числа с остатком и без остатка, делитель и частное.
Теоретический материал темы: четные и нечетные числа, признаки делимости натурального числа на 2, 3, 5, 10 без остатка.
Применение изученного материала: ближайшая перспектива (простые и составные числа, разложение на простые множители, НОД, взаимнопростые числа, НОК), дальнейшая перспектива (отношения и пропорции).
4. Цели изучения темы:
Обучающие: сформулировать понятие четного и нечетного числа, сформулировать признаки делимости, научить правильно воспроизводить термины, правила, приводить примеры; сформировать умение применять изученный материал при решении поставленных задач.
Развивающие: развитие познавательных процессов, памяти, внимания, математического мышления, восприятия; развитие устной и письменной речи.
Воспитательные: воспитание интереса к математике и учебной деятельности; воспитание отдельных качеств личности: усидчивости, трудолюбия, аккуратности и упорства.
5. Типы учебных задач:
Типы учебных задач для достижения развивающих целей.
На развитие внимания.
1. Найдите среди чисел 154, 161, 174, 178, 191, 315, 320, 346, 425, 475 числа:
А) кратные 2; б) кратные 5; в) кратные 10; г) нечетные.
2. Какие из чисел 241, 242, 244, 246, 248, 250, 252 на 3?
3. Ученики условливаются о каком-то однозначном числе, например, 3. Ученики считают попорядку натуральные числа: 1, 2, 3, 4, … . Ученик, которому по очереди досталось сказать три, а также числа, которые начинаются с цифры три, или оканчиваются цифрой три, или делятся на три, должен вместо этого сказать «гоп».
Типы задач для достижения воспитательных целей.
На воспитание интереса к математике.
1. Какие из чисел 200, 320, 3000, 50000, 861, 76540 делятся на 100? Какие из них делятся на 100? Сформулируйте признаки делимости на 100, на 1000.
2. Любое ли число, которое оканчивается цифрой 3, делится на 3?
3. Подумайте, каким числом (четным или нечетным) является:
А) квадрат четного числа;
Б) квадрат нечетного числа;
В) куб четного числа.
4. Как быстро узнать , делятся ли на 3:
А) 37843+54321; 48345+75634; 37244+52486;
Б) 87338-56893; 153847-112353; 84537-26237?
5. найдите пропущенные цифры:
Курс математики обладает большим гуманитарным потенциалом: история математики, исторические и занимательные задачи, текстовые математические задачи самого разного содержания. Это дает возможность ставить цели воспитания и развития интереса к математике и учебной деятельности в целом.
Средства формирования познавательно интереса.
Ø Занимательные задачи.
Примеры задач с историческим содержанием.
1.Рассказывают, что в начальной школе, где учился мальчик Карл Гаусс, ставший потом знаменитым математиком, учитель, чтобы занять класс на продолжительное время самостоятельной работой, дал детям задание – вычислить сумму всех натуральных чисел от 1 до 100. Но маленький Гаусс это задание выполнил почти моментально. Попробуйте и вы быстро выполнить это задание.
2.У известного русского художника Богдана – Бельского есть картина, изображающая занятия устным счетом. В классе возле доски сидит учитель, а около него стоят ученики, занятые устном решением трудного примера. Ученики сосредоточены и увлечены работой, так как пример действительно труден и интересен.
 Вот он:
Вот он: 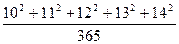 . Решите этот пример устно.
. Решите этот пример устно.
[Указание. Искомое число равно 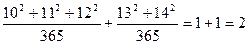 .]
.]
Ø Задачи с историческим содержанием.
Ø Задачи Пифагора.
Ø Дидактические игры.
Лабиринт сомножителей.В воротах лабиринта стоят делители числа 432 (рис. 5). Поочередно члену каждой команды надо войти в лабиринт и дойти до центра, получив в произведении число 432. Движение можно выполнить и в обратном направлении. Побеждает та команда, у которой будет наибольшее число правильных ответов.
Фрагмент урока изучения новой темы: «Признаки делимости на 2, 3, 5, 10».
Образовательные:
Обучающие:
обеспечить в ходе урока усвоения признаков делимости на 2, 3, 5, 10, формировать умение правильно воспроизводить термины, признаки, приводить примеры, формировать умение применять изученный материал при решении поставленных задач.
Развивающие: способствовать развитию мышления, восприятия, памяти, внимания, диалектического мировоззрения.
Воспитательные: воспитывать устойчивый интерес к математике, воспитывать отдельные качества личности: настойчивость, трудолюбие, усидчивость, упорство.
Тип урока: изучение нового материала
Структура урока:
· организационный момент
· постановка целей урока
· проверка домашнего задания
· подготовка к изучению нового материала
· изучение нового материала
· первичное закрепление и осмысление нового материала
· постановка домашнего задания
· подведение итогов урока.
| Действия учителя | Действия учеников |
| Здравствуйте, ребята. На прошлом уроке мы узнали какие числа называются делителями, а какие кратными. Давайте сейчас вспомним какое число называется делителем данного натурального числа? Какое число является делителем любого числа? Какое число называется кратным натуральному числу а? Какое число и кратно n, и является его делителем n? Но для того, чтобы определить является ли число делителем заданного натурального числа или кратным ему не всегда нужно выполнять арифметические действия. Как это сделать мы и узнаем сегодня на уроке. Запишите тему урока: признаки делимости на 2, 3, 5, 10. | Делителем натурального числа а называют натуральное число, на которое а делится без остатка. Число 1 Кратным натуральному числу а называют натуральное число, которое делится без остатка на а. Само число n |
Билет № 21.
Дата добавления: 2021-12-14; просмотров: 769;











