Билет №20. Арифметические приложения теории сравнений
Определение 10.1.Функцией Эйлера называется функция  :N® N, где
:N® N, где  (m) (m
(m) (m  N)равно количеству взаимно простых с m натуральных чисел, не превосходящих m.
N)равно количеству взаимно простых с m натуральных чисел, не превосходящих m.
Иначе,  (m) (m
(m) (m  N) есть количество натуральных чисел k, удовлетворяющих условиям:
N) есть количество натуральных чисел k, удовлетворяющих условиям:
1 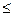 k
k 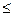 m, (k, m) = 1.
m, (k, m) = 1.
Примеры.  (1)=1. Среди чисел 1, 2, 3, 4, 5, 6, 7, 8 взаимно простыми с 8 являются лишь 1, 5, 7. Поэтому
(1)=1. Среди чисел 1, 2, 3, 4, 5, 6, 7, 8 взаимно простыми с 8 являются лишь 1, 5, 7. Поэтому  (8)=3.
(8)=3.
Замечание. Функция Эйлера мультипликативна, т.е. для любых двух натуральных взаимно простых чисел а и b имеем  (a∙b) =
(a∙b) =  (a) ∙
(a) ∙  (b).
(b).
Например,  (6)=
(6)=  (2∙3) =
(2∙3) =  (2) ∙
(2) ∙  (3) = 1 ∙ 2 = 2.
(3) = 1 ∙ 2 = 2.
Свойства функции Эйлера описываются следующей теоремой.
Теорема 10.1.Если p – простое, то
1)  (p) = p – 1; 2)
(p) = p – 1; 2)  (p
(p 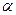 ) = p
) = p 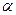 -1(p – 1).
-1(p – 1).
3) Для любого натурального m 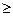 2 выполняется равенство
2 выполняется равенство
 (m) = m ∙
(m) = m ∙ 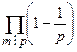
Иначе, если m = 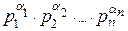 , то
, то  (m) = m ∙
(m) = m ∙ 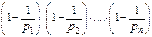 .
.
Доказательство. 1) Для каждого простого числа p лишь одно из чисел среди 1, 2, …, p не взаимно просто с p, а именно само число p. Поэтому  (p) = p – 1.
(p) = p – 1.
2) Если m = p 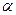 есть степень простого числа, то нетривиальный общий делитель с m могут иметь лишь числа, делящиеся на p, т.е. числа вида pk. Неравенство 1
есть степень простого числа, то нетривиальный общий делитель с m могут иметь лишь числа, делящиеся на p, т.е. числа вида pk. Неравенство 1 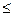 pk
pk 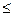 p
p 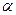 выполняется лишь для натуральных чисел k
выполняется лишь для натуральных чисел k 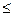 p
p 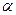 -1 и только для них. Поэтому
-1 и только для них. Поэтому
 (p
(p 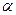 ) = p
) = p 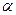 – p
– p 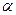 -1.
-1.
3) Пусть m = 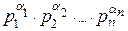 . В силу мультипликативности функции Эйлера имеем:
. В силу мультипликативности функции Эйлера имеем:  (m) =
(m) = 
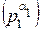 ∙
∙ 
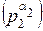 ∙ … ∙
∙ … ∙ 
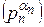 =
= 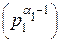 ∙ (p1 - 1) ∙ ∙
∙ (p1 - 1) ∙ ∙ 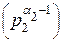 ∙ (p2 - 1) ∙ … ∙
∙ (p2 - 1) ∙ … ∙ 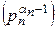 ∙ (pn - 1) = m ∙
∙ (pn - 1) = m ∙ 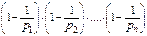 .
.
Примеры.Вычислить:
1)  (7). 7 – простое число, поэтому
(7). 7 – простое число, поэтому  (7) = 7 – 1 = 6.
(7) = 7 – 1 = 6.
2)  (125). 125 = 53, потому
(125). 125 = 53, потому  (125) =
(125) =  (53) = 53-1∙(5 – 1) = 100.
(53) = 53-1∙(5 – 1) = 100.
3)  (84). Найдем каноническое разложение 84. 84 = 22 ∙ 3 ∙ 7.
(84). Найдем каноническое разложение 84. 84 = 22 ∙ 3 ∙ 7.
 (84) =
(84) =  (22 ∙ 3 ∙ 7) = 84 ∙
(22 ∙ 3 ∙ 7) = 84 ∙ 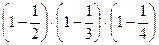 = 24.
= 24.
Дата добавления: 2021-12-14; просмотров: 684;











