Свойства скалярного произведения

1⁰. Скалярный квадрат а²= а×а вектора а равен квадрату длины вектора: а² = |a|².

Непосредственно следует из определения: а² = а×а = |a|×|а|×cos 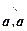= |a|²×cos 0 = |a|² .

2⁰. Вектор нулевой тогда и только тогда, когда его скалярный квадрат равен нулю: а = 0 Û а² = 0.

В самом деле, а = 0 Û |a| = 0 Û |a|² = 0 Û а² = 0.

3⁰. Скалярное произведение векторов не зависит от порядка перемножаемых векторов: а×b = b×a .

Непосредственно следует из определения: а×b = |a|×|b|×cos 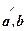= |b|×|a|×cos 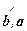= b×a .

4⁰. Если a(x; y; z) и b(u; v; w) – векторы, координаты которых вычислены относительно некоторой декартовой системы координат, то а×b = x×u+y×v+z×w.

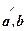По теореме косинусов для D АВС (см. рис.) имеем: |b–a|² = |a|²+|b|²–2|a|×|b|×cos , т.е. a×b = 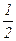×{|a|²+|b|²–|b–a|²}. Если бы уже была доказана формула |c| = 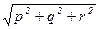для вычисле­ния длины вектора c(p; q; r) по его декартовым ко­ор­динатам p, q, r, то учтя, что b–a(u–x; v–y; w–z), сразу получили бы

a×b = 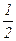×{x²+y²+z²+u²+v²+w²– –(u–x)²–(v–y)²–(w–z)²} = 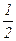×{2×(x×u+y×v+z×w)} =x×u+y×v+z×w , что и

требовалось.

Таким образом, остаётся обосновать использованную формулу для длины вектора в декартовых координатах.

Лемма (о вычислении длины вектора в декартовых координатах). Пусть c(p; q; r) – вектор, координаты которого вычислены в некоторой декартовой системе координат. Тогда |c| = .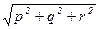

Доказательство. Отложив вектор c = 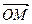от начала координат, получим по теореме Пифагора: |c|² = OM² = OM¢ ²+MM¢ ² = OA¢ ²+OB¢ ²+ MM¢ ² = (p×OA)²+(q×OB)²+(r×OC)² = = p²×1²+q²×1²+r²×1² = p²+q²+r², что и требовалось. Лемма доказана.

5⁰. Скалярное произведение векторов линейно по обоим аргументам: (a+b)×с = a×c+b×c, a×(b+c) = a×b+a×c.

В самом деле, записав векторы в координатах a(x; y; z), b(u; v; w), c(p; q; r) в некоторой декартовой системе координат, получим (a+b)(x+u; y+v; z+w), (b+c)(u+p; v+q; w+r) и по 4⁰ (a+b)×с =(x+u)×p+(y+v)×q+(z+w)×r = (x×p+y×q+z×r)+(u×p+v×q+w×r) = a×c+b×c, a×(b+c) = x×(u+p)+ +y×(v+q)+z×(w+r) = (x×u+y×v+z×w)+(x×p+y×q+z×r) = a×b+a×c, что и требовалось.

6⁰. Скалярное произведение однородно по обоим аргументам: (l×a)×b = l×(a×b) = a×(l×b).

Следует из определения:например, (l×a)×b = |l×a|×|b|×cos 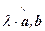= |l|×|a|×|b|×sg(l)×cos 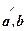= = l×(a×b), где sg(l) – знак числа l (почему cos 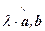= sg(l)×cos ?!?).

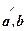7⁰. Если известны декартовы координаты векторовa(x; y; z) и b(u; v; w), то угол между ними можно вычислить по формуле 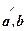= arccos 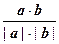=arc cos .

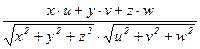8⁰. Два вектора a(x; y; z) и b(u; v; w), координаты которых заданы в декартовой системе координат ортогональны тогда и только тогда, когда x×u+y×v+z×w = 0.

Действительно a ^ b Û a×b = 0 Û x×u+y×v+z×w = 0.

Задача. Докажите, что прямоугольный параллелепипед ABCDA₁B₁C₁D₁ является кубом тогда и только тогда, когда углы между его длинная диагональ AC₁ образует равные углы с рёбрами АА₁ , АВ и AD.

Решение.Рассмотрим декартову систему координат, начало которой совпадает с вершиной А , а оси направлены по прилегающим к А рёбрам параллелепипеда. Если длины этих рёбер a, b, c, то A(0; 0; 0), B(a; 0; 0), D(0; b; 0), A₁(0; 0; c), C₁(a; b; c), 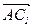(a; b; c), и условия равенства углов с осями записываются в виде равенства косинусов углов между 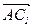и базисными векторами i, j, k : 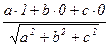= = = 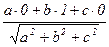. Ясно, что эти равенства равносильны равенству длин всех рёбер параллелепипеда.