Простые и составные числа
Определение 9.1.Натуральное число p называется простым, если оно имеет только два различных между собой натуральных делителя: 1и p.
Примеры.2, 3, 5, 7, 11, 13– простые числа.
Определение 9. 2. Натуральное число, большее единицы, называется составным, если оно имеет более двух различных натуральных делителей.
Примеры.4, 6, 8, 9, 10, 12 – составные числа.
Замечание 1.Из этих определений следует, что множество натуральных чисел можно разбить на три класса:
а) составные числа;
б) простые числа;
в) единица.
Если а – составное, то а = nq, где 1 < n < a, 1 < q < a.
Простейшие свойства простых чисел
10. Если а 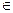 Z и p – простое, то (а, p) = 1
Z и p – простое, то (а, p) = 1 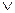 а
а 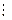 p.
p.
Действительно, пусть d = (a, p), тогда (а 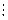 d)
d) 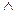 p
p 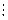 d, т.к. p – простое число, то оно имеет два делителя 1 и p. Если (а, p) = 1, то а и p взаимно просты, а если (а, p) = p, то а
d, т.к. p – простое число, то оно имеет два делителя 1 и p. Если (а, p) = 1, то а и p взаимно просты, а если (а, p) = p, то а 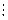 p.
p.
20. Если произведение нескольких сомножителей делится на p, то, по крайней мере, один из сомножителей делится на p.
Действительно, пусть произведение а1 ∙ а2 ∙ … ∙ аn делится на p. Если предположить противное: все аi не делятся на p, то (а1 ∙ а2 ∙ … ∙ аn, p) = 1, следовательно, какой-то сомножитель делится на p.
30. Различные простые числа взаимно просты.
40. Наименьший простой делитель p натурального числа n > 1 не превосходит 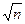 .
.
Пусть n = p ∙ n1, причем p 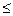 n1 и p – простое. Тогда n
n1 и p – простое. Тогда n 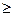 p2
p2 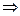 p
p 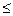
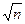 .
.
50. Если натуральное число n не делится ни на одно простое число p 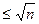 , то n – простое, в противном случае оно будет составным.
, то n – простое, в противном случае оно будет составным.
Данное свойство непосредственно следует из свойства 40.
Пример. Выясним, будет ли число 157 простым?
Выпишем простые делители, не превосходящие 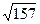 : 2, 3, 5, 7, 11. Проверяем, что 157 не делится на 2, на 3, на 5, на 7, на 11. Следовательно, число 157 – простое.
: 2, 3, 5, 7, 11. Проверяем, что 157 не делится на 2, на 3, на 5, на 7, на 11. Следовательно, число 157 – простое.
Решето Эратосфена
На свойстве 50 основан метод, позволяющий определить список простых чисел p1 < p2 < … до заданной границы n. Этот метод носит название решето Эратосфена, названный в честь древнегреческого математика, географа и астронома.
Шаг 1. Выпишем подряд все натуральные числа 2, … , n – 1, n.
Положим, что p1 = 2 и вычеркнем все последующие числа, делящиеся на 2, кроме p1 = 2.
Шаг 2. Пусть k 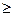 2 и уже определены числа p1,…, pk-1. Обозначим pk первое невычеркнутое число, следующее за pk-1. Если pk2 > n, то обозначим pk+1, pk+2, … все оставшиеся невычеркнутыми числа, следующие за pk, в порядке возрастания. На этом алгоритм завершает свою работу.
2 и уже определены числа p1,…, pk-1. Обозначим pk первое невычеркнутое число, следующее за pk-1. Если pk2 > n, то обозначим pk+1, pk+2, … все оставшиеся невычеркнутыми числа, следующие за pk, в порядке возрастания. На этом алгоритм завершает свою работу.
Шаг 3. Если pk2 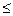 n, то вычеркиваем числа, делящиеся на pk, начиная с pk2 (двигаясь до n с шагом pk). Вычеркнутые ранее числа также принимаются в учет, но не вычеркиваются еще раз. По завершении процедуры алгоритм увеличивает индекс k на единицу и переходит к шагу 2.
n, то вычеркиваем числа, делящиеся на pk, начиная с pk2 (двигаясь до n с шагом pk). Вычеркнутые ранее числа также принимаются в учет, но не вычеркиваются еще раз. По завершении процедуры алгоритм увеличивает индекс k на единицу и переходит к шагу 2.
В результате алгоритм оставляет невычеркнутыми только простые числа.
Примеры: 1.Найти все простые числа, меньшие 30.
Применим решето Эратосфена, остановившись, как только найдём простое число, не меньшее 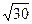 = 5,…, т.е. простое число 7.
= 5,…, т.е. простое число 7.

Теорема Евклида. Основная теорема арифметики
Теорема 9.1 (теорема Евклида). Множество простых чисел бесконечно.
Доказательство.
Предположим противное, пусть p1, p2, … , pk – все простые числа, где p1 = 2, а pk – самое большое простое число.
Составим натуральное число n = p1 · p2 · … · pk + 1, т.к. n > pi, то оно должно быть составным. Покажем, что наименьший делитель q 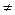 1 числа n будет простым. Так как n – составное, то n = n1 ∙ q, где q < n1. Если предположить, что q – составное число, то q = q1 ∙ k и n = n1 ∙ q1 ∙ k, так как q1 < q, то q – уже не будет наименьшим делителем числа n, что противоречит условию. Итак, наименьший делитель числа n будет простым. Однако n не делится ни на p1, ни на p2, … , ни на pk, так как 1 не делится на любое pi .
1 числа n будет простым. Так как n – составное, то n = n1 ∙ q, где q < n1. Если предположить, что q – составное число, то q = q1 ∙ k и n = n1 ∙ q1 ∙ k, так как q1 < q, то q – уже не будет наименьшим делителем числа n, что противоречит условию. Итак, наименьший делитель числа n будет простым. Однако n не делится ни на p1, ни на p2, … , ни на pk, так как 1 не делится на любое pi .
Следовательно, наше предположение о конечности множества простых чисел было неверно.
Замечание 2. Простые числа составляют лишь небольшую часть чисел натурального ряда. Доказано, что в натуральном ряду существуют сколь угодно длинные интервалы, не содержащие ни одного простого числа.
Теорема 9. 2 (основная теорема арифметики). Любое натуральное число n > 1 может быть представлено единственным образом в виде произведения простых чисел, с точностью до порядка сомножителей.
Доказательство.
I. Докажем возможность представления методом математической индукции по величине числа. Пусть n 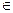 N и n > 1.
N и n > 1.
1) n = 2. Утверждение выполняется, так как 2 – простое число.
2) Предположим, что утверждение теоремы выполнено для всех натуральных чисел,меньших числа k.
3) Покажем, что утверждение выполнено для k.
а) Если k – простое число, то доказывать нечего.
б) Если k – составное число, то оно имеет делитель а, такой, что 1 < a < k . Тогда k = a ∙ b. Очевидно, что 1 < b < k. Согласно предположению, теорема выполнена для чисел а и b, т. е. а = p1 ∙ p2 ∙ … ∙ ps и b = q1 ∙ q2 ∙ … ∙ qm, где pi, qj – простые. Тогда k = p1 ∙ p2 ∙ … ∙ ps ∙ q1 ∙ q2 ∙ … ∙ qm. Полученная формула означает, что существует представление числа k в виде произведения простых чисел.
Согласно принципа математической индукции возможность представления в виде произведения простых чисел доказана для любого натурального n > 1.
II. Покажем, что представление числа n в виде произведения простых чисел единственно с точностью до порядка сомножителей.
Пусть n = p1 ∙ p2 ∙ … ∙ ps и n = q1 ∙ q2 ∙ … ∙ qr, где pi, qj – простые числа, тогда будет иметь место равенство:
p1 ∙( p2 ∙ … ∙ ps) = q1 ∙ q2 ∙ … ∙ qr (1)
Тогда простое число p1 делит q1 ∙ q2 ∙ … ∙ qr, так что p1 делит одно из простых чисел правой части, пусть q1 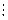 p1 , а значит, p1 = q1 . Поэтому обе части рассматриваемого равенства можно сократить на p1. Разделив обе части равенства (1) на p1, получим равенство p2 ∙ … ∙ ps = q2 ∙ … ∙ qr . Повторяя процесс рассуждения еще (s – 1) раз, мы получим равенство:
p1 , а значит, p1 = q1 . Поэтому обе части рассматриваемого равенства можно сократить на p1. Разделив обе части равенства (1) на p1, получим равенство p2 ∙ … ∙ ps = q2 ∙ … ∙ qr . Повторяя процесс рассуждения еще (s – 1) раз, мы получим равенство:
1 = qs+1 ∙ qs+2 ∙ …∙ qr
Так как все qi > 1, то это равенство невозможно. Следовательно, в обеих разложениях число сомножителей одинаково (s = r) и сами сомножители одинаковы.
Замечание 3. В разложении числа n на простые сомножители некоторые из них могут повторяться. Обозначим буквами 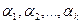 кратность их вхождения в n, получим так называемое каноническое разложение числа n:
кратность их вхождения в n, получим так называемое каноническое разложение числа n:
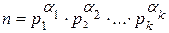
Дата добавления: 2021-12-14; просмотров: 578;











