Билет № 14. Алгебра матриц

Примерный план ответа

Сформулировать определения операций над матрицами, привести примеры, сформулировать свойства, доказать теоремы о векторном пространстве матриц одинаковой размерности и кольце квадратных матриц n-го порядка над полем P, обосновать один из способов вычисления обратной матрицы и матричный способ решения системы линейных уравнений.

Кольцо матриц M_{m n}(F) и векторное пространство матриц M_{m n}(F)

Определение 4.1.Пусть F – некоторое поле, m, n Î N. Прямоугольная таблица вида 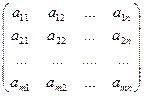, где a_ij Î F (1 £ i £ m,1 £ j £ n), называется прямоугольной (m´ n) - матрицей над полем F с элементами a_ij и обозначают короче || a_ij || или буквами А, В, С, ...

Любая строка этой матрицы есть n-мерный арифметический вектор, а любой столбец – m-мерный арифметический вектор.

Множество всех (m´ n)-матриц над полем F будет обозначаться через M_{m n}(F). В случае m = n матрица называется квадратной порядка n.

Определение 4.2.Две матрицы A, B ÎM_{m n}(F)называются равными (пишут А = В), если a_ij = b_ij (1 £ i £ m,1 £ j £ n).

Другими словами, две матрицы равны тогда и только тогда, когда они имеют одинаковые размерности и равные соответствующие элементы.

На некоторых подмножествах множества M_{m n}(F)можно определить две бинарные операции (+ , ·) и две унарные операции (умножение на скаляр и нахождение обратной матрицы).

Определение 4.3.Суммой матриц A = || a_ij ||, B = || b_ij ||ÎM_{m n}(F) называется матрица С = A+B = || a_ij || + || b_ij ||= || a_ij+b_{i j} ||Î M_{m n}(F) (1 £ i £ m,1 £ j £ n).

Определение 4.4.Произведением матрицы A = || a_ij || ÎM_mn(F) на скаляр a Î F называется матрица a × A= ||a × a_ij ||ÎM_{m n}(F) (1 £ i£ m,1 £ j £ n).

Определение 4.5.Произведение матриц A = || a_is || Î M_mk (F) и B = || b_sj ||, B ÎM_{k n}(F) – это матрица С = A× B = || c_ij ||= || a_i1 · b_1j+ a_i2 · b_2j + … + a_ik · a_kj ||, СÎM_mn(F) (1 £ i £ m,1 £ j £ n,1 £ s £ k ).

Замечание. Сложение матриц и умножения матриц на скаляры являются алгебраическими операциями на M_mn(F) – множестве матриц одинаковой размерности m × n, а умножение матриц является алгебраической операцией только на множестве M_nn(F) квадратных матриц порядка n.