Определение и простейшие свойства векторных пространств. Примеры
Пусть V – непустое множество, состоящее из элементов произвольной природы. Будем обозначать его элементы малыми буквами латинского алфавита, и называть векторами. Пусть дано произвольное поле F = (F, +, ·), элементы которого будем обозначать малыми буквами греческого алфавита, и называть скалярами.
Зададим на множестве V бинарную операцию +: V×V 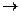 V, +: (а, b)
V, +: (а, b) 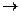 с, где а, b, c
с, где а, b, c  V и назовем ее сложением векторов (
V и назовем ее сложением векторов ( а, b
а, b  Vа + b
Vа + b  V).
V).
Определим также внешнюю композицию w 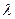 : F × V
: F × V 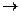 V , w
V , w 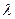 : (
: ( 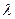 , а)
, а) 
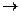
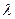 а
а
и назовем ее умножением скаляра на вектор (
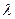
 F
F  а
а  V
V 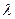 а
а  V).
V).
Определение. 3.1.Алгебра V = (V, +, {w 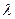 |
| 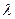
 F}) называется векторным (линейным) пространством над полем F, если выполняются следующие условия (аксиомы):
F}) называется векторным (линейным) пространством над полем F, если выполняются следующие условия (аксиомы):
1 – 4. (V, +) – абелева группа.
5.  а
а  V 1 ∙ а
V 1 ∙ а  V.
V.
6. 
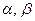
 F
F а
а  V (
V ( 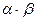 ) ∙ а =
) ∙ а = 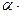 (
( 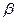 ∙а) (умножение на скаляр ассоциативно).
∙а) (умножение на скаляр ассоциативно).
7. 
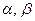
 F
F а
а  V (
V ( 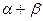 ) ∙ а=
) ∙ а= 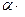 а +
а + 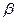 ∙ а (умножение на скаляр дистрибутивно по отношению к сложению векторов).
∙ а (умножение на скаляр дистрибутивно по отношению к сложению векторов).
8. 

 F
F  а, b
а, b  V
V  ∙ (а + b) =
∙ (а + b) = 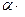 а +
а +  ∙ b (умножение вектора на скаляр дистрибутивно по отношению к сложению скаляров).
∙ b (умножение вектора на скаляр дистрибутивно по отношению к сложению скаляров).
Замечание 1. Если F = R, то V над R называют вещественным векторным пространством, если F = C, то V над C называют комплексным векторным пространством.
Примеры. 1. Rn – арифметическое векторное пространство, в котором любой вектор а  Rnпредставляет собой упорядоченный набор из n действительных чисел, то есть а = (
Rnпредставляет собой упорядоченный набор из n действительных чисел, то есть а = ( 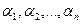 ), где
), где 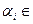 R(i = 1, 2, … , n); в Rn операция сложения векторов и умножение на скаляр задается правилами:
R(i = 1, 2, … , n); в Rn операция сложения векторов и умножение на скаляр задается правилами:
а) a + b = ( 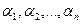 ) + (
) + ( 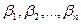 ) = (
) = ( 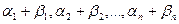 );
);
б) 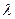 · а =
· а = 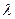 · (
· ( 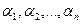 ) = (
) = ( 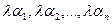 ).
).
2. Мnn(R) – векторное пространство квадратных матриц n-го порядка над полем R. Любой вектор в этом пространстве представляет собой квадратную матрицу вида:
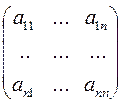
А + B = || aij || + || bij || = || aij + bij || , i, j = 0, 1, 2,…, n; 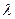 · || aij || = ||
· || aij || = || 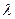 аij ||.
аij ||.
3. V2 – векторное пространство геометрических векторов плоскости.
4. V3 – векторное пространство геометрических векторов трехмерного пространства.
Замечание 2.Из определения следует, что любое векторное пространство V надFпрежде всего является аддитивной абелевой группой, поэтому все свойства абелевых групп справедливы и для векторных пространств.
В след. теореме сформулируем простейшие свойства (следствия из определения V над полем F).
Теорема 3.1.Если V векторное пространство над полем F, то  а, b
а, b  V,
V, 
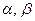
 F:
F:
10. (a + b = a) 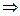 (b =
(b = 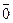 )
)
20. (a + b = 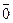 )
) 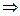 (b = – a)
(b = – a)
30. (  a =
a =  b
b 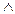

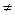 0)
0) 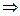 (a = b)
(a = b)
40. (  a =
a = 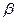 a
a 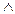 a
a 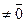 )
) 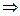 (
( 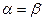 )
)
50. (  a =
a = 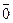 )
) 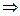 (
(  = 0
= 0 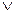 a =
a = 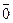 )
)
60. 0∙ a = 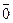
70.  ∙
∙ 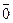 =
= 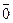 .
.
Для доказательства всех этих утверждений используются свойства аддитивной группы векторного пространства и другие аксиомы.
10. Действительно, (a + b = a) 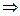 (b =
(b = 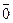 ), так как (V, +) – абелева группа, в которой существует единственный
), так как (V, +) – абелева группа, в которой существует единственный 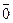
 V :
V :  а
а  V a +
V a + 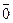 = а.
= а.
20. Аналогично в группе (V, +)  а
а  V
V 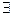 !(-а )
!(-а )  V:а + (- а) = (- а) + а =
V:а + (- а) = (- а) + а = 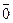 , следовательно, b = - a.
, следовательно, b = - a.
30. (  a =
a =  b
b 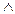

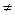 0)
0) 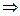 (a = b) так как
(a = b) так как 
 F , а F – поле, то в нем
F , а F – поле, то в нем 

 F (
F ( 
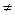 0)
0) 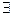
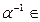 F
F  ·
· 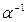 =
= 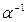 ·
·  = 1 и тогда
= 1 и тогда 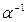 ·(
·(  а) =
а) = 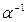 ·(
·(  b)
b) 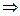
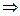 (
( 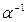 ·
·  ) а = (
) а = ( 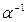 ·
·  ) b
) b 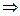 (a = b).
(a = b).
60. 0 ∙ a = 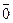 . Действительно, 0 · а = (0 + 0) · а = 0 · а + 0 · а, отсюда по свойству 10 следует, что 0 · а =
. Действительно, 0 · а = (0 + 0) · а = 0 · а + 0 · а, отсюда по свойству 10 следует, что 0 · а = 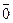 .
.
Аналогично можно доказать остальные свойства.
Дата добавления: 2021-12-14; просмотров: 495;











