Алгебраическая система

Определение 6.1. Множество Μ вместе с заданными на нем операциями {φ1, φ2,...,φ n} называется алгеброй. Обозначение алгебры: 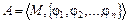, где М называется основным множеством (несущим множеством, носителем), а 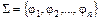- сигнатурой алгебры A.

Примером алгебры является полугруппа - множество Μ с заданной на нем одной бинарной ассоциативной операцией (обозначается: · ), т.е. A= {М; ·}, например множество натуральных чисел N с операцией сложения + на нем, т.е. A= {Ν; +} является полугруппой.

Типом алгебры A называется вектор парностей операций сигнатуры. Например, в алгебре A= {R; +, χ}, где R - множество действительных чисел, + и χ - соответственно операции сложения и умножения (такая алгебра называется полем действительных чисел), сигнатура Σ = {+, χ} включает две бинарные операции - сложение и умножение. Поэтому тип данной алгебры (2,2).

Определение 6.2. Алгебраическую систему 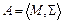, где множество 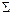состоит из одной двухместной операции, называется группоидом.

Определение 6.2. кольцом называется алгебра с двумя операциями 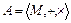, если обладает следующими свойствами:

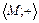- - Авелева группа

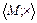- - полугруппа

- Операция умножения дистрибутивна относительно сложения ( ).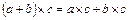

Определение 6.3. Множество Μ вместе с заданными на нем отношениями {R₁ R₂, ..., R_n} называется моделью. Обозначение модели: 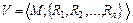, где М - несущее множество (универсум), 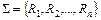– сигнатура модели V. Например, моделью V₁| является мно­жество М₁, чисел с отношениями: "быть больше" (>) и "быть равным" (=), т.е. V₁ = (M₁; >, =), или некоторое множество M_г людей с отношением R - "быть руководителем", т.е. V_г = (М₂; R), и т.д.

Определение 6.4. Множество Μ вместе с заданными на нем операциями {φ₁, φ₂, ..., j_n} и отношениями {R_1, R₂, ···,R_n} называется алгебра­ической системой, или алгебраической структурой. Обозначение алгебраической структуры:

V= (Μ; φ₁, φ₂,..., φ_n; R₁, R₂,..., R_n).

Если полугруппа обладает коммутативным свойством ( 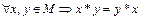), то её называют Авелевой группой.

Примером алгебраической структуры является так назы­ваемая решетка - множество Μ с заданными на нем: одним бинарным отношением частичного порядка (обозначение ≤) и двумя бинарными операциями ( ∩ и U ): {М;≤; ∩, U }.

Таким образом, алгебры - это алгебраические структуры с пустым множеством отношений. Другим частным случаем алгебраических структур являются модели, т.е. множества, на которых заданы только отношения.