Геометрическая интерпретация действий

Операции над комплексными числами также могут быть осмыслены с геометрической точки зрения. Так, операции сложения z₁ + z₂ (вычитания z₁ – z₂ = z₁ + (– z₂ ) двух комплексных чисел z₁ и z₂ в алгебраической записи соответствуют операции сложения двух векторов по правилу параллелограмма (рис. 3).

При умножении двух комплексных чисел в тригонометрической форме их модули перемножаются, а аргументы складываются. Следовательно, чтобы умножить комплексное число z₁ на z₂ нужно длину вектора z₁ изменить в | z₂ | раза (растянуть или сжать), а затем полученный вектор повернуть вокруг начала координат на угол arg z₂ (рис. 4)

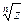Геометрический смысл операции состоит в делении окружности радиуса 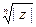на n равных частей.

Пример.Вычислить 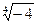и изобразить все его значения геометрически.

Представим комплексное число z = – 4 в тригонометрической форме. Для этого найдем его модуль и аргумент.

| – 4 | = 4, arg (– 4) = 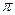, – 4 = 4 (cos 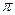+ i · sin )

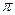Тогда 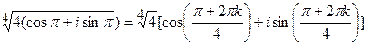, k = 0, 1, 2, 3.

Придавая параметру k значения 0, 1, 2, 3, получаем четыре значения корня четвертой степени из 4.

z₀ = ,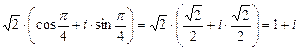

z₁ = ,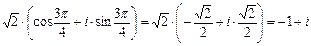

z₂ = ,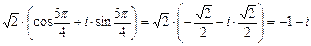

z₃ = .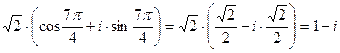

Изобразим найденные корни на комплексной плоскости, они делят окружность радиуса 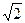на четыре равные части. Кроме того, мы вписали в эту окружность правильный четырехугольник (квадрат) (рис. 5).

Замечание. Часто при решении задач используется геометрический смысл модуля разности двух комплексных чисел, как расстояния между двумя точками на плоскости. | z₁ – z₂ | = 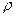( z₁, z₂).

Пример.Найти геометрическое место точек, для которых

| z – (2 + i) | 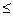3

y

Геометрический смысл этого неравенства состоит в том, что расстояние от точки (2, 1) до точек (x, y) не превосходит 3. Это значит, что искомым геометрическим местом точек является круг с центром в точке (2, 1) радиуса 3 (рис. 6).

МЕТОДИКА 12.