Алгебраическая форма

Векторная (геометрическая) форма

Пусть имеется система, например, четырех сходящихся сил 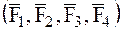, действующих на НМС (МТ) (рис. 13).

На основании следствия из аксиомы 2 перенесем силы вдоль линии их действия в точку пересечения этих линий, и последовательно сложив все силы по правилу треугольника, получим силовой многоугольник (рис. 13).

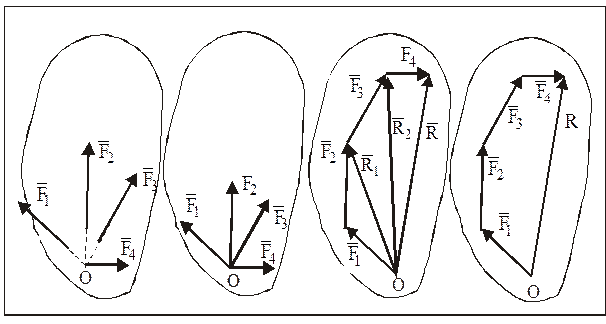Рис. 13

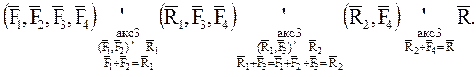
Таким образом, можно записать:

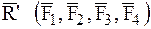или .

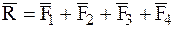Аналогично для системы n сходящихся сил, получим:

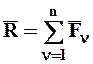. (2.1)

Система сходящихся сил всегда приводится к одной силе – равнодействующей этой системы сил, которая является замыкающей стороной силового многоугольника, построенного на этих силах, и равна геометрической сумме этих сил.

Для пространственной системы сходящихся сил силовой многоугольник является пространственной фигурой, для плоской - плоской фигурой.

Алгебраическая форма

Выбрав декартовую систему координат с началом в точке пересечения линий действия сил и спроектировав соотношение (2.1) на ее оси, получим проекции равнодействующей пространственной системы сходящихся сил на эти оси:

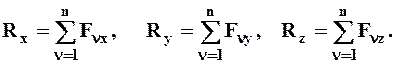(2.2)

Модуль равнодействующей определяется соотношением:

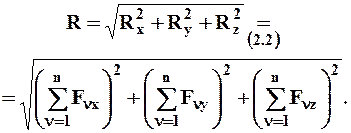(2.3)

Направление равнодействующей определяется направляющими косинусами:

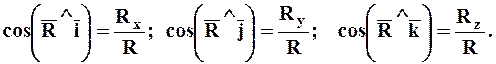(2.4)

Для плоской системы сходящихся сил в соотношениях (2.2)–(2.4) 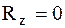, если плоская система сил находится в плоскости xОy.