Теорема о поле комплексных чисел
Назовем мнимой единицей символ i, удовлетворяющий единственному свойству: i2 = – 1.
Теорема 2.1. Существует единственное, с точностью до изоморфизма поле (С, +, ×), называемое полем комплексных чисел, в котором выполняются следующие условия:
1. Поле действительных чисел (R, +, × ) является подполем в (С, +, × ),
2.$ i Î Ci2 = –1.
3." z ÎC$ ! a, b Î R z = a + i× b.
Запись комплексного числа z в виде a + i× b называется его алгебраической формой записи, при этом а называют действительной частью комплексного числа z, i× b – мнимой частью, а b – коэффициентом мнимой части.
Обозначение: Re z – действительная часть, I m z – мнимая часть комплексного числа.
При доказательстве этой теоремы устанавливаются следующие правила сложения, умножения и деления в поле комплексных чисел для чисел в алгебраической форме записи:
(a + i × b) + (c + i × d) = (a + c) + i × (b + d), (1)
(a + i× b) × (c + i× d) = (a × c – b × d) + i × (a × d + b × c), (2)
(a + i × b) – (c + i × d) = (a – c) + i × (b –d), (3)
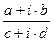 =
= 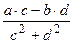 + i ×
+ i × 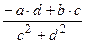 ,где на(c + i × d)
,где на(c + i × d) 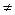 0 (4)
0 (4)
На практике обычно формулы (3) и (4) не запоминают, а руководствуются такими мнемическими правилами:
а) чтобы перемножить два комплексных числа, нужно перемножить их как два двучлена;
б) чтобы разделить(a + i × b)на(c + i × d) 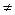 0, нужно числитель и знаменатель домножить на комплексное число , сопряженное знаменателю и выполнить указанные действия ((c – i × d) называют сопряженным по отношению к (c + i × d)).
0, нужно числитель и знаменатель домножить на комплексное число , сопряженное знаменателю и выполнить указанные действия ((c – i × d) называют сопряженным по отношению к (c + i × d)).
Примеры. 1. (2 + i · 5) + (3 + i · (-4)) = (2 + 3) + i · (5 – 4) = 5 + i
2. (2 + i × (–3)) × (1 – i) – 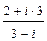 = (–1 – i × 5) –
= (–1 – i × 5) – 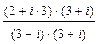 = (–1 – i × 5) – –
= (–1 – i × 5) – – 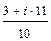 =
= 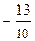 + i × (
+ i × ( 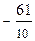 ) .
) .
Так как (z = a + i · b)  (C = R × R), то с геометрической точки зрения, любое комплексное число имеет две равноправные геометрические интерпретации (модели).
(C = R × R), то с геометрической точки зрения, любое комплексное число имеет две равноправные геометрические интерпретации (модели).
1) точка координатной плоскости А (а, b);
2) радиус-вектор 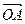 с концом в точке с координатами (а, b).
с концом в точке с координатами (а, b).
Дата добавления: 2021-12-14; просмотров: 667;











