Вычисление дуги кривой линии.

Длина отрезка вычисляется по формулам:1. 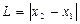и 2.

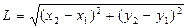
Теорема: Если ф-ция f(x) и её производная 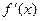непрерывна на отрезке [a,b], то длина кривой (дуги): 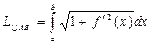- в прямоугольных координатах.

б)ПустьАВ задана своими параметрическими уравнениями: 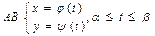, тогда .

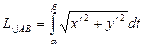МЕТОДИКА 10. Логико – математический анализ теоретического материала темы

Основные понятия темы:

· Первообразная;

· Криволинейная трапеция;

· Интеграл функции (пределы интегрирования, знак интеграла, подынтегральная функция, переменная интегрирования).

Основные предложения темы:

· Признак постоянства функции;

· Теорема (основное свойство первообразных);

· Правила нахождения первообразных;

· Теорема (вычисление площадей криволинейных трапеций): .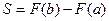

· Если 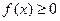на отрезке [a;b], то площадь S соответствующей криволинейной трапеции выражается формулой S= .

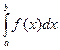· Если F - первообразная для f на отрезке [a;b], то 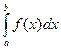= 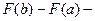формула Ньютона – Лейбница. Она верна для любой функции f, непрерывной на отрезке [a;b].

· Замечание: удобно расширить понятие интеграла, полагая по определению при 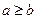, что .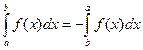

· Геометрический смысл основного свойства первообразных: графики любых двух первообразных для функции получаются друг из друга параллельным переносом вдоль оси OY.

Результаты логико – математического анализа можно представить в виде таблицы: