Свойства определённого интеграла

1⁰ Т: Если ф-ция f(x) на отрезке [a,b], то она на нём интегрирована.

2⁰ Постоянный множитель выносится за знак интеграла: .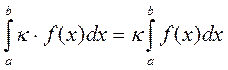

3⁰Определённый интеграл от алгебраической суммы ф-ций равен алгебраической сумме интегралов слагаемых: .

4⁰Если на отрезке [a,b], где ф-ции f(x), g(x) связаны f(x)≤g(x), то таким же знаком неравенства связаны и их интегралы: .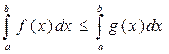

5⁰ Если на отрезке [a,b] ф-ция f(x) ограничена m≤f(x)≤M, a<b, .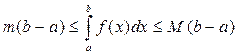

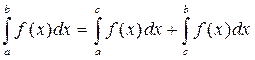6⁰ Для справедливо неравенство: , где .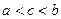

7⁰ Если на отрезке [a,b] ф-ция f(x) положительна, то интеграл так же положителен : .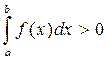

8⁰ Если поменять местами пределы интегрирования, то опред. интеграл меняет знак: .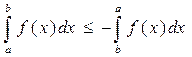

9⁰Опред-й интеграл с одинаковыми пределами интегрирования равен нулю: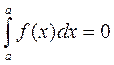

10⁰ .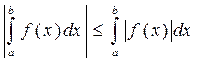

11⁰ Теорема о среднем значении:Если ф-ция f(x) непрерывна на отрезке [a,b], то найдётся такая (.)с, что справедливо неравенство: 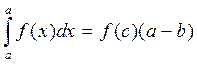, где .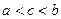

Формула Ньютона-Лейбница.Известно, что если ф-ция f(x) непрерывна на отрезке [a,b], то одной из её первообразных явл-ся 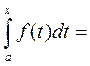Ф(х). Также известно, что любые две первообразные отличаются на константу, т.е. пусть F(x)- любая первообразная для f(x) на [a,b] 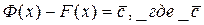- конкретное число. Положим, что в этой формуле х=а , ,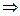

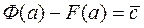
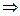
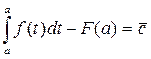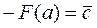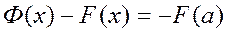
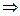
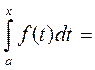
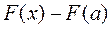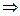
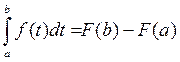
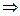
, положим, что х=b формула Ньютона-Лейбница.