Простейшие свойства групп, колец, полей

1⁰. Единичный элемент в группе единственен.

2⁰. Обратный элемент к любому элементу группы определён однозначно.

3⁰.В любой группе выполняется следующий обобщённый закон ассоциатив­­ности: " k Î N" a₁ , … , a_k Î G произведение a₁* … *a_k не зависит от расстановки скобок.

4⁰. В любой группе (G, *) выполняются законы сокращения слева и справа:

" f, g, h Î G f * g = f * h 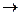g = h, " f, g, h Î G f * h = g * h 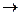f = g .

5⁰. В любой группе однозначно разрешимы уравнения a * x = b и y * a = b, где а, b – произвольные элементы.

6⁰. " k 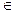N " g₁ , … , g_k Î G (g₁* … *g_k)^–1 = g_k^–1* … *g₁^–1.

7⁰. Аддитивная группа (K, +) любого кольца удовлетворяет 1⁰–6⁰.

8⁰. В любом кольце выполняется обобщённый закон ассоциатив­­ности умножения.

9⁰. " a, b Î K (– a)× b = a× ( – b)

10⁰. Для кольца с единицей: " a Î K – a = (–1)× a

В любом кольце определяется операция вычитания: a – b = a + (– b)

11⁰. " a, b, c Î K a × (b – c) = a× b – a × c, " a, b, c Î K (a – b)× c = a× c – b× c

12⁰. " a₁ , … , a_n , b Î K (a₁ ± a₂ ± …± a_n )× b = a₁× b ± a₂ × b ± …± a_n× b, b× (a₁ ± a₂ ± … ± a_n ) = b× a₁ ± b× a₂ ± … ± b × a_n

13⁰. Любое поле удовлетворяет всем свойствам колец.

14⁰. Если (F, +, ×) – поле и F^* = F \ {0} то (F^* , ×) – группа, называемая мультипликативной группой поля.

В любом поле определяется операция деления на ненулевые элементы:

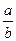= a× b^–1.

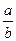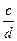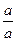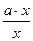15⁰. Свойства дробей в поле: = Û a× d = b× c, = 1, = a, = , ± = , × = , = .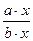

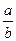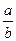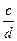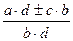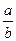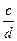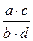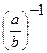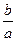Гомоморфизмы групп, колец, полей

Определение 1.7. Пусть (A, *)и (B,Ä) – группы. Отображение j : A ® B называется гомоморфизмом групп, если оно сохраняет операцию, т.е. " x, y Î A j(x * y) = j (x)Äj (y).

Определение 1.8. Если (A, +, ×)и (B, Å, Ä) – кольца, то отображение j : A ® B называется гомоморфизмом колец, если оно сохраняет обе операции, т.е.

" x, y Î A j (x + y) = j(x) Åj (y)," x, y Î A j (x × y) = j (x) Ä j (y).

Определение 1.9. Инъективные гомоморфизмы называют мономорфизмами или вложениями, сюръективные гомоморфизмы – эпиморфизмами или наложениями, а биективные – изоморфизмами.

Определение 1.10. Если существует гомоморфизм групп или колец j : А ® B, то группы или кольца А, В называют изоморфными.

Смысл изоморфизма состоит в том, что он устанавливает такое соответствие между элементами изоморфных объектов, которое показывает, что с точки зрения сохраняемых алгебраических операций изоморфные объекты неразличимы.

Примеры: 1.Тождественный изоморфизм I: A ® A ," x Î A I (x) = x. (A – группа или кольцо).

2. Единичный или нулевой эпиморфизм: если E = {e} – одноэлементный объект (единичная группа или нулевое кольцо), то для любой группы (A, *)или кольца определён эпиморфизм О: A ® E, " x Î A О(x) = e.

3. Естественные вложения групп и колец: Z® Q ® R ® C.