Место темы в программе, учебниках математики
Пропедевтика элементов математического анализа (производной и интеграла) проводится при изучении функций в основной школе.
Тема «Интеграл» изучается в 11 классе по учебнику Алгебра и начала анализа: Учеб.для 10-11 кл.общеобразоват.учреждений/Ш. А. Алимов, Ю. М. Колягин и др.-10-е изд.-М.:Просвещение, 2002
2. Виды планирования темы, примерная структура тематического плана
| Тема | Подтема | Задачи | Теоретич. материал | Задачи в классе | Задачи дома | Повторение | С/Р | Формы контроля |
| Интеграл | Правила нахождения первообразных | Ввести правила нахождения первообразных, научить применять правило на практике | Таблица первообразных | 988; 989(1,2,3); 992(1,2). | 989(4,5,6); 990(1,2,3); 992(3,4). | Опрос, индивидуальная проверка | ||
| Решение задач | Закрепить данные правила в процессе решения задач. Осуществить контроль за состоянием знаний и умений по теме. | 993; 994(1,3); 995(1,2). | 994(2,4); 995(3,4); 996. | (для сильных учащихся) | Проверка д/з, с/р. |
3. Опишите технологический подход к планированию темы
Технологическая карта (педагогическая технология В.М.Монахова). Тема: Интеграл (11 класс).
| Логическая структура учебного процесса | В1 Д1 В2 Д2 | |
| Целеполагание | Диагностика | Коррекция |
| В1. Знать определение криволинейной трапеции. Уметь распознавать к.т. и вычислять ее площадь. | С/р1. Вычислить площадь к.т., ограниченной линиями:
· y=x3+1, y=0, x=0, x=2
· y=cos x, y=0, x=0, x= 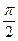 · y=x2, y=0, x=0, x=3
· y=x2, y=0, x=0, x=3
| Возможные ошибки: · при выполнении рисунка (неверное изображение графиков функций); · в нахождении первообразных; · вычислительные, при вычислении S к.т.; Замечание: учебные задачи для коррекции составляются для предупреждения и устранения каждого вида ошибки. |
| В2. Знать формулу Ньютона – Лейбница, применять ее к вычислению S фигуры, ограниченной линиями. Уметь вычислять S фигуры. | С/р2.
1. Вычислить интегралы:
· 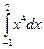 ·
· 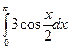
| Возможные ошибки: · в нахождении первообразных; · выбор неправильной фигуры для вычисления S. · В применении формулы Ньютона - Лейбница |
| Дозирование самостоятельной деятельности учащихся | ||
| Удовлетворительно | Хорошо | Отлично |
Вычислить площадь фигуры, ограниченной линиями:
· 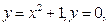 x=-1, x=2;
· x=-1, x=2;
· 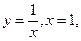 x=3,y=0. x=3,y=0.
| Вычислить площадь фигуры, ограниченной линиями: · y=x2-x-5, y=x-2 · y=x2+x-4, y=6-x2 | Вычислить площадь фигуры, ограниченной линиями:
· y=x2, 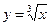 · y=sin x,
· y=sin x, 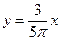
|
Вычислить интегралы:
· 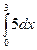 ·
· 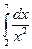
| Вычислить интегралы:
· 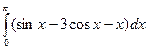 ·
· 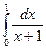
| Вычислить интегралы:
· 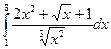 ·
· 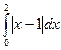
|
Дата добавления: 2021-12-14; просмотров: 547;











