Основные свойства неопределённого интеграла

1⁰Производная неопределённого интеграла равна подынтегральной ф-ции: .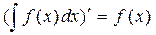

2⁰ Дифференциал от неопределённого интеграла равен подынтегр-му выр-нию: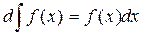

3⁰ Постоянный сомножитель выносится за знак неопред-ного интеграла: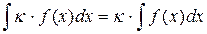

4⁰ Неопределённый интеграл от алгебраической суммы ф-ций равен алгебраической сумме интегралов слагаемых: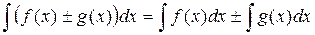

5⁰ Неопределённый интеграл от дифференциала для любой ф-ции равен самой этой ф-ции плюс константа: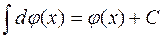

Интегрирование по частям - это один из самых распространённых методов интегрирования. Формула интегрирования по частям: .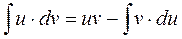

(п2) 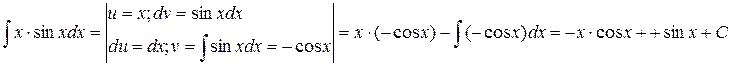Интегрирование методом замены переменной (метод подстановки) - при этом методе данный интеграл приводится к другому интегралу с другой переменной интегрирования. Замена переменных осуществляется следующим образом:

Пусть дан интеграл у= 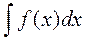, который не вычисляется с помощью непосредственного интегрирования и интегрирования по частям и пусть ф-ция x=φ(t) – явл-ся строго монотонной и дифференцируемой.

Найдём 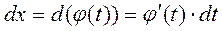, тогда данный интеграл равен следующему интегралу : 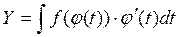. Окончательно имеем: .

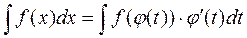Замечание: полученный интеграл обязательно д/б проще, чем данный интеграл.

Гораздо чаще встречается подстановка иного типа.

Пусть дан интеграл: 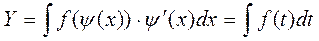, тогда замена переменной будут такой: 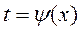- часть подынтегральной ф-ции обозначается ч/з новую переменную:

(п2)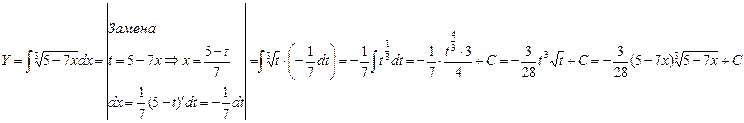

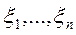Определённый интеграл.Пусть на отрезке [a,b] задана непрерывная ф-ция f(x) и [a,b] разбит на части. В каждом элементарном отрезке [х₀, х₁],…, [х_n-1, х_n] произвольно выберем по одной точке (кси): . Найдём значение ф-ции в выбранных точках 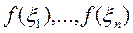и составим интегральную сумму: 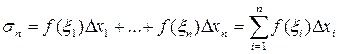. Она зависит от способа разбиения на элементарные части и от выбора точек 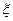-тоя. Нижняя и верхняя суммы Дарбу явл-ся частным случаем интегральной суммы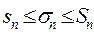

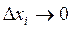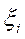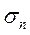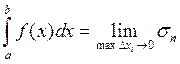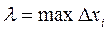
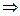
Представим себе, что отрезок [a,b] делится на бесконечное число элементарных частей и длина каждой из них → 0. Если при любых разбиениях [a,b], таких, что максимальное значение и при любом выборе точек на элементарном отрезке, интегральная сумма стремится к одному и тому же пределу, то он наз. определённым интегралом ф-ции f(x) на отрезке [a,b] и обозначается: , обозначим , где а – нижний, b- верхний предел интеграла, f(x)- подынтегральная ф-ция х- переменная интегрирования.

Если предел существует, то ф-ция f(x) наз. интегрированной на отрезке [a,b].

Геометрический смысл: Если f(x)≥0, то определённый интеграл представляет собой площадь криволинейной трапеции сверху ограниченную графиком ф-ции у= f(x), снизу осью Ох, слева прямой х=а и слева х=b.