Введение поправок в измеренную длину линии. Определение неприступных расстояний. Дальномеры

1. Учет поправок при линейных измерениях. Точность измерений

В измеренное значение длины линии вводят следующие поправки:

ΔD_k – поправка за компарирование,

ΔD_t – поправка за температуру,

ΔD_ν – поправка за наклон линии.

,

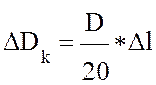гдеD –длина измерительной линии,

Δl –поправка за компарирование.

Если поправка положительная, то есть длина ленты больше 20 м, то поправка прибавляется, если отрицательная –отнимается.

,

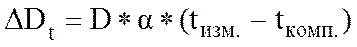α –линейный коэффициент расширения стали (12*10^-6);

поправка за температуру вводится если(t_изм. – t_комп.) > 8º.

;

;

;

;

.

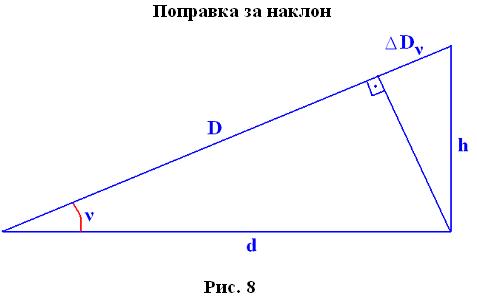
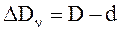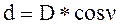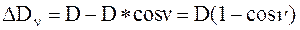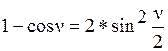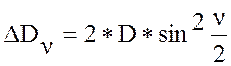Тогда в общем виде:

.

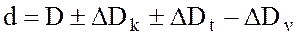При измерении длин линий не только мерной лентой, но и другими мерными приборами (рулетками, инварными проволоками) вводятся те же поправки.

Точность измерений линий лентой зависит главным образом от характера местности:

при идеальных условиях – 1/3000;

при средних условиях – 1/2000;

при неблагоприятных условиях – 1/1000.

Например: точность 1/2000 означает: на 100 м ± 5 см.

2. Определение неприступных расстояний

В некоторых случаях, вследствие каких–либо препятствий, измерить линию продольного хода непосредственно лентой невозможно.

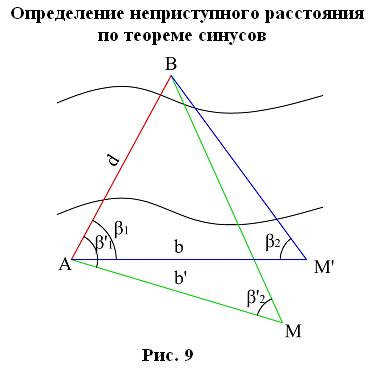
2.1. 1–й случай: (точка В недоступна для линейных измерений). По теореме синусов

Разбиваем на местности ≈ равносторонний треугольник. Измеряем углы: ß₁,ß₂,ß'₁,ß'₂ и базисы b₁,b ₂.

Тогда неприступное расстояние АВ определяется по теореме синусов:

;

;

.

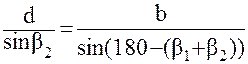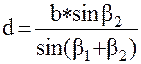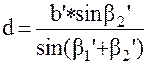При заданной точности измерения базисов 1:2000, предельное расхождение между двумя определениями d не должно превышать 1:1000. За окончательное значение берется среднее из двух определений.

2.2. 2–й случай: (между точками нет взаимной видимости). По теореме косинусов

Разбиваем на местности примерно равнобедренные треугольники ABC, ABC₁.

Этот способ применяется, когда между точками A и В нет взаимной видимости.

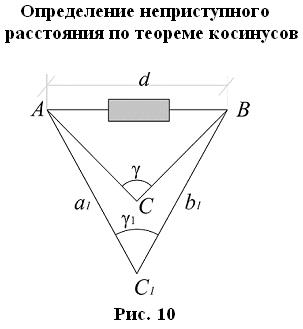
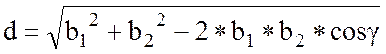
Измеряются базисы: a₁,a ₂,b₁,b ₂.

Расстояние определяется по теореме косинусов.

Расстояние определяется дважды.

Расхождение между двумя определениями – 1/1000.

За окончательное значение берется среднее.

5. Оптические дальномеры

Наиболее распространенным типом дальномеров является нитяной.

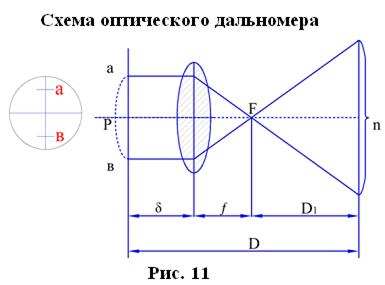
Здесь р – расстояние между дальномерными нитями;

n– количество делений дальномерной рейки между дальномерными нитями;

р – коэффициент дальномера, который обычно равен100;

n – количество делений дальномерной рейки, видимых в трубу между дальномерными нитями.

Расстояние с помощью нитяного дальномера определяется по формуле:

.

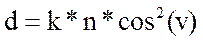При измерении наклонных расстояний дальномером визирный луч направлен наклонно.

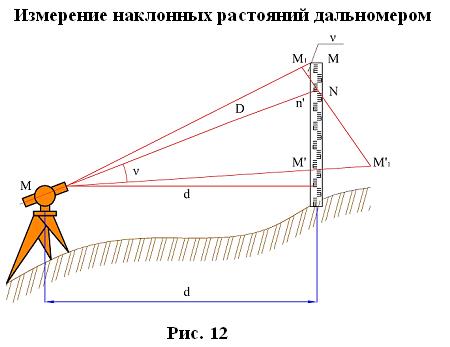
Если бы рейка стояла перпендикулярно лучу MN, то взяв по рейке отчет n', мы определили бы расстояние:

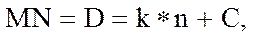
где C – постоянное слагаемое дальномера.

В действительности же рейка всегда ставится вертикально и берется отчет n. Считая треугольник прямоугольным, получим:

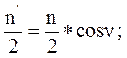
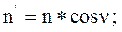
Следовательно:

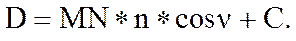
Тогда горизонтальная проекция dравна:

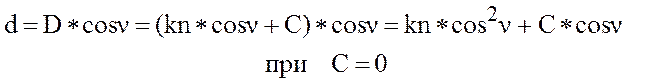
Исследованиями установлено, что точность измерения расстояний нитяным дальномером при использовании технических теодолитов ≈ 1/300.

С другими оптическими дальномерами можно ознакомиться в учебнике Д.А. Кулешова,Г.Е. Стрельникова «Инженерная геодезия для строителей».

В настоящее время для определения расстояний разработаны светодальномеры и лазерные дальномеры. Устройство этих приборов основано на измерении времени, необходимого для прохождения электромагнитных волн в прямом и обратном направлениях.

Считая, что скорость распространения электромагнитных волн V известна, можно записать:

.

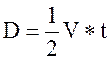Прибор состоит из приемопередатчика, установленного на начальной точке, и отражателя, установленного на конечной точке линии.

Скорость распространения электромагнитных волн в вакууме:

V = 2997925 ± 0,4 км/c.

ЛЕКЦИЯ 12