Фрагмент урока на этапе усвоения понятия
Тема: Геометрическая прогрессия
Тип урока: изучение нового материала
Цели урока:
Образовательные:
· ввести понятие геометрической прогрессии
· формировать умения решать прикладные задачи с использованием данного понятия.
Развивающие:
· развивать познавательные интересы: память, внимание, восприятие;
· развивать логическое мышление
Воспитательные:
· воспитание интереса к математике
· воспитывать отдельные качества личности: трудолюбие, аккуратность, настойчивость.
Структура урока:
1. Организационный момент (2 мин)
2. Подготовка к изучению нового материала (5 мин)
3. Изучение нового материала (10 мин)
4. Усвоение нового материала (15 мин)
5. Постановка домашнего задания (5мин)
6. Подведение итогов урока (3 мин)
  Треугольник равносторонний, со стороной 2 см.
Треугольник равносторонний, со стороной 2 см.
| Тема: Геометрическая прогрессия | № 406, 407, 409, 412. |
| Деятельность учителя | Деятельность учащихся |
| Давайте рассмотрим следующую последовательность –10, 20, – 40, …; Запишите, как получен каждый последующий член 20 = – 10 * … – 40 = 20 * … Чему равен знаменатель q? Что надо знать, чтобы записать формулу n-го члена геометрической прогрессии? Какие задачи можно решать, применяя эти формулы? Для закрепления изученного материала, мы с вами прорешаем несколько примеров, номера которых записаны на доске. № 406 решим устно: Назовите первый член и знаменатель геом. прогрессии: 1) 4, 2, 1, ….; 2) -10, 20, -40, …; 3) -50, 10, -2, …; Оставшиеся номера решаем у доски и самостоятельно в тетради. № 407. Записать первые пять членов геом. прогрессии, если: 1) b1 = 12, q =2 2) b1 = -3, q = -4 Аналогично решаем следующие номера по данным формулам. | Внимательно слушают учителя и отвечают на вопросы учителя рассматривают последовательность вида –10, 20, – 40, ….; 20 = – 10 * (-2) – 40 = 20*(-2) q=-2 b1; q; n – первый член прогрессии, знаменатель, и номер данного члена прогрессии. bn=b1qn-1 – на нахождение знаменателя, найти номер члена данной геом. прогрессии, чему он равен. Решают № 406 устно 1) 4 и ½ 2) -10 и -2 3) -50 и -5 Решают № 407 в тетради и у доски 1) b1 = 12 b2=12*2=24 b3=24*2=48 b4=48*2=96 b5=96*2=192 2) b1 = -3 b2=-3*(-4)=12 b3=12*(-4)=-48 b4=-48*(-4)=192 b5=192*(-4)=-768 Решают номера, записанные на доске № 406, 407, 409, 412. |
Билет № 9.«Множество и его мощность».
Множество – это неопределяемое понятие, оно является первичным. Его смысл можно понять лишь на примерах или найти слова синонимы – совокупность, набор. А, В, С, Х,У – множества, а его элементы А ={х, у, z, t}, где х 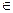 А.
А.
Два множества равны, если они состоят из одних и тех же элементов.
Множество В явл-ся подмножеством А, если каждый элемент мн-ва В явл-ся и элементом множества А (А 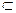 В, т.е. А содержит в себе В).
В, т.е. А содержит в себе В).
Над множеством можно производить следующие действия: объединение, пересечение, разность
Множество С явл-ся объединением мн-в А и В, если оно принадлежит А или В.
(п2) A={2}, В={3,4,5} 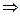 С=А
С=А 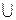 В={2,3,4,5}.
В={2,3,4,5}.
Пересечением мн-в А и В наз. мн-во С, которое состоит из тех элементов, которые 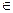 А и В.
А и В.
(п3) A={2,3,7}, В={3,4,5} 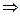 С=А
С=А 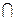 В={3}.
В={3}.
Разностью мн-в А и В наз. мн-во С, которое состоит из тех элементов, которые 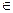 А, но
А, но 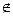 В.
В.
(п4) A={2,3,7,16}, В={3,4,5,16}  С=А/В={2,7}, С=В/А={4,5}.
С=А/В={2,7}, С=В/А={4,5}.
Мн-во наз. ограниченным, если оно расположено на отрезке, т.е. 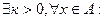 /x/
/x/  к
к 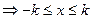
Мн-во наз. ограниченным сверху, если 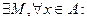 x≤М.
x≤М.
Мн-во наз. ограниченным снизу, если 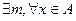 : x≥m.
: x≥m.
Мн-во наз. ограниченным сверху и снизу, если 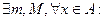 m
m 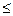 x
x 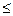 М.
М.
Мн-ва бывают конечные, бесконечные (п6) и пустые (не имеют элементов и явл-ся подмножеством любого мн-ва, н/р, мн-во корней уравнения х2+4=0).
Когда имеются конечные мн-ва, то их можно сравнивать по числу элементов.
(п5) А содержит - n1элементов и В - n2 (n1=n2, n1>n2, n1<n2 ).
Если мн-ва бесконечны, то сравнивать их по числу элементов нельзя. В этом случае можно применить другой способ – ВОС. Два множества наз. эквивалентными, если между их элементами можно установить взаимно однозначное соответствие, где каждому элементу одного множества соответствует единственный элемент другого и обратно.
(п6) A={a,b,c,d,e,f}~ B={а,б,в,г,д,е}- конечные множества.
A={1,2,3,4,…,n,…}~ B={1,4,9,16,…,n2,…}- бесконечные множества (n→n2).
Бесконечные мн-ва А и В имеют одинаковую мощность или явл-ся эквивалентными, если между ними установлено ВОС ((п6) m(А)=m(В)). Мощность – это то общее, что характеризует все эквивалентные между собой мн-ва.
(п7) А~В1, В1 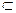 В, mА<mВ или В~А1, А1
В, mА<mВ или В~А1, А1 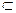 А, mА>mВ.
А, mА>mВ.
Любое бесконечное мн-во, эквивалентное мн-ву всех натуральных чисел наз. счётным мн-вом.
(п8) N={1,2,3,4,…,n,…}~ A={1,4,9,16,…,n2,…},(n↔n2), А~N→ А – счетное мн-во.
Мощность мн-в натуральных чисел явл-ся самой маленькой для бесконечных мн-в m(A)=a. Поэтому мощность любого счётного мн-ва равна а.
Свойства счётных множеств:
10 Для того чтобы мн-во А было счётным необходимо и достаточно, чтобы все его элементы могли быть представлены в виде последовательности, т.е. перенумеровать с помощью мн-ва натуральных чисел.
20 Из всякого бесконечного мн-ва можно выделить счётное мн-во.
30 Любое бесконечное подмножество счётного мн-ва также счётно.
40 Объединением конечного числа счётных мн-в явл-ся счётным мн-вом.
50 Объединение счётного мн-ва конечных мн-в также счётно.
60 Объединение счётного мн-ва счётных мн-в также счётно.
70 Если бесконечное мн-во А={ai,k}, где ai,k – элементы мн-ва А (i,k 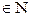 ),то А счётное мн-во.
),то А счётное мн-во.
80 Мн-во всех рациональных чисел счётно.
Док-во: Q=Q+ 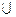 Q-
Q- 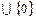 -нейтр. эл-т Q+=
-нейтр. эл-т Q+= 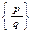 ,
, 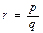 - рац. число (p,q
- рац. число (p,q 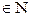 ).
).
Q+={ap,q}- то по св-ву 7 это мн-во счётное  Q- - счётно
Q- - счётно  Q+
Q+ 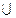 Q-
Q- 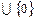 - счётно
- счётно
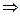 Q – счётное мн-во.
Q – счётное мн-во.
Теорема1: Мн-во целых чисел явл-ся счётным мн-вом.
Из бесконечных мн-в нам известно счётное, но существуют другие бесконечные мн-ва – несчётные, н/р, мн-во всех действительных чисел между 0 и 1. Мн-во наз. несчётным, если оно бесконечное, но счётным не явл-ся.
Теорема2: Мн-во действительных чисел на отрезке [0;1] несчётно.
Док-во: (метод от противного)
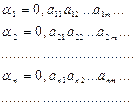 Предположим, что мн-во всех R на [0;1] – счётно
Предположим, что мн-во всех R на [0;1] – счётно 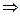 все элементы этого мн-ва можно перенумеровать с помощью мн-ва всех N чисел.
все элементы этого мн-ва можно перенумеровать с помощью мн-ва всех N чисел.
A= 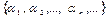 - счётное
- счётное
Создадим число
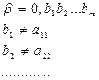 (b1 – любая цифра)
(b1 – любая цифра) 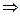
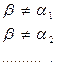
Число 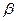 не вошло в мн-во А, т.е. предположение было неверным, т.о. мн-во А – счётно
не вошло в мн-во А, т.е. предположение было неверным, т.о. мн-во А – счётно
МЕТОДИКА 9.
Изучение рациональных чисел начинается в 6 классе. Понятие о рациональных числах вводится в теме «Положительные и отрицательные числа». И только в 8 классе, вводятся понятия, «дробные выражения», «рациональные дроби», и действие с дробями.
Цели изучения темы
Обучающие цели: - Обеспечить усвоение понятий: положительные и отрицательные числа, противоположные числа, модуль числа, координатная прямая и правила сравнения чисел;
- Научить правильно, воспроизводить термины, определения понятий, приводить примеры;
- Формировать умения записывать и читать положительные и отрицательные числа, противоположные числа, модуль числа, умение сравнивать положительные и отрицательные числа;
- Формировать умения решать типовые арифметические задачи;
Развивающие цели: - Развивать познавательные процессы: внимание, восприятие, память.
- Развивать мышление: умение сравнивать, обобщать, формулировать правила, алгоритмы, делать индуктивные умозаключения;
- Развивать речь, мировоззрение, умение учиться.
Воспитательные цели: - Воспитывать интерес к математике и учебной деятельности через использование исторических и занимательных задач.
- Воспитывать культуру общения, общую культуру.
- Воспитывать отдельные качества личности (настойчивость, трудолюбие).
Урок закрепления
Структура: -Проверка Д\З; - Сообщение темы , цели, мотивация; - Решение задач в стандартных ситуациях; -Применение знаний, в новых, в измененных ситуациях; -Подведение итогов; -Д\З
Цели урока: систематизация и обобщение знаний учащихся по теме;
- развитие логического мышления, аргументированной математической речи;
- повышение интереса к предмету;
- воспитание честности во время взаимоконтроля.
Фрагмент: Тестирование. Проверку осуществляет противоположный вариант и выставляет оценки.
Учащимся раздаются тесты на 2 варианта.
Вариант 1. Какие из равенств верны? а) |3| = 3 ; б) |-3|= 3 ; в) |-3|= -3
2. Верно ли расположены в порядке возрастания числа 0; -5; 3?
3.Чему равно значение выражения -7 + 7? а) 14; в) 0; с) -14; д) нет правильного ответа.
4. Найдите: -27 + 7. а) -36; в) -22; с) 22; д) нет правильного ответа.
5. Найдите: -13 – 47. а) -34; в) 50; с) -50; д) нет правильного ответа.
Критерии оценки.
- “5” - за все правильно выполненные задания;
- “4” - если допущена одна ошибка;
- “3” - если допущено две ошибки;
Примерная методическая схема изучения рациональных дробей в школе.
1вводится понятие дробного выражения и рациональной дроби. (дается определение);2устанавливается правило сокращения дробей и основное свойство дроби;3определяются операции: сложение, вычитание, умножение, деление.В каждой из этих групп выражении изучается их определение, классификация, выделяются выражение стандартного вида или простейшего, изучаются тождественные преобразования.
Основные типы задач.задачи – примеры, в записи условий которых используются только математические символы( цифры, знаки действия, скобки), а словесный текст, как правило отсутствует. Метод их решения – выполнение арифметических действий с учетом правил об их порядке.задачи – расчеты – задачи межпредметного и прикладного характера, иногда с готовой формой расчета. После составления числового выражения приводится к задаче – примеру и решается тем же методом.Текстовые сюжетные задачи более сложного математического характера, которые в большинстве случаев легко решаются алгоритмически, но, если не пользоваться уравнением, представляющие собой некоторые трудности и требующие для решения сообразительности.Стандартные:1) Преобразуйте в дробь выражение. 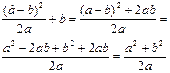 Нестандартные:Туристы прошли s км по шоссе со скоростью v км/ч и вдвое больший путь по проселочной дороге. Сколько времени t (в часах) затратили туристы, если известно, что по проселочной дороге они шли со скорость, на 2км/ч меньшей, чем по шоссе?
Нестандартные:Туристы прошли s км по шоссе со скоростью v км/ч и вдвое больший путь по проселочной дороге. Сколько времени t (в часах) затратили туристы, если известно, что по проселочной дороге они шли со скорость, на 2км/ч меньшей, чем по шоссе?
Билет № 10. «Интеграл».
Пусть дана ф-ция у=f(x) заданная на отрезке [a,b], будем считать, что эта ф-ция непрерывна на нём, тогда F(x) наз. первообразной ф-цией для ф-ции f(x) на отрезке [a,b], если 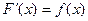 .
.
(п1) f(x)=х3 F(x)= 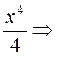
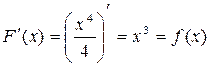
Мн-во всех первообразных ф-ции f(x) наз. неопределённым интегралом и обозначается: 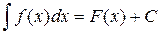 , где f(x) – подынтегральная ф-ция, f(x)dx – подынтегральное выражение, а х – переменная интегрирования.
, где f(x) – подынтегральная ф-ция, f(x)dx – подынтегральное выражение, а х – переменная интегрирования.
Дата добавления: 2021-12-14; просмотров: 446;











