Линейное дифференциальное уравнение I порядка (ур-ия Бернулли)

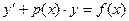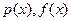Линейное д/у I порядка наз. уравнение , где - данные известные ф-ции. Искомая ф-ция у и её производная 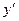не должны умножаться друг на друга и делится.

Линейное дифференциальное уравнение интегрируется несколькими способами: метод Бернулли и метод вариации произвольной постоянной.

Общее решение данного урав-я ищется в виде произведения двух ф-ций 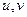, пока неизвестных: 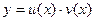или 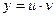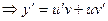. Подставим значения для у и 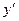в данное уравнение: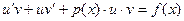

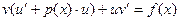
Пр: 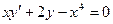Приведём данное уравнение к стандартному виду, т.е. разделим на х:

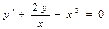
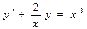- линейное д/у I порядка. Ищем общее решение: ,

/

/

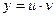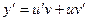
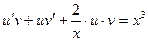
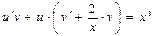
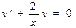
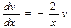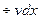
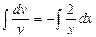
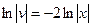
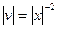
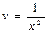
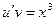
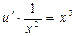
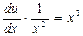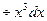
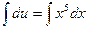
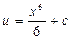
Ответ: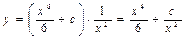

3. Тема: «Простейшие дифференциальные уравнения».Тип урока: изучение нового материала (урок-практикум).Класс: 11 класс (математического профиля). Учебник: Ш.А.Алимов, Ю.М.Колягин, Ю.В.Сидоров. Алгебра и начала анализа.Обучающие:формировать умение решать задачи на дифференцирование и интегрирование;выделить разные виды решения задач, расширить кругозор учащихся.Воспитательные: воспитание внимательности, аккуратности, трудолюбия;воспитание интереса к предмету.Развивающие:развивать коммуникативные способности;развивать креативность мышления; расширить кругозор учащихся.Структура урока:Организационный момент;Сообщение темы урока, постановка целей урока;Объяснение нового материала;Закрепление нового материала (решение практических задач);Подведение итогов урока;Домашнее задание.Психологическая характеристика юношеского возрастаСтабилизация многих физиологических функций, формирование телесной конституции, свойственной взрослому человеку, позволяет юношам и девушкам учувствовать в различных видах производственного труда. Трудовая деятельность способствует обогащению теоретических знаний, полученных во время учебы, расширению кругозора, а главное – формированию качеств необходимых для будущей профессиональной деятельности, для самореализации. Необходимость выбора дальнейшего жизненного пути, избрание той или иной профессии является наиболее важной особенностью этого возраста.Черты личности в юношеском возрасте определяются теми психологическими новообразованиями, которые зарождаются еще в подростковом возрасте: усиление интереса к своей собственной личности, стремление к самостоятельности взрослости; проявление критичности и т.д., но они несколько видоизменятся. У человека основным содержанием деятельности является труд, создание материальных и духовных ценностей. Отношение индивида к виду опосредуется теперь его отношением к обществу и культуре. Отсюда – качественно иное, чем у животных, содержание понятий созревание и подготовка к жизни. Созревание предполагает, таким образом, социализацию, и не может осуществляться вне её и помимо её. Поэтому и переходный возраст это этап развития личности, процесс перехода от зависимого, опекаемого детства, когда ребенок живет по правилам взрослых, к самостоятельной и ответственной деятельности взрослого человека.В психолого-педагогической литературе акцент делается не на физическом развитии, а на смене ведущих форм деятельности. Божович Л.И. определяет старший школьный возраст как юношеский, сосредоточив свое внимание на: развитии мотивационной сферы личности; определение старшеклассников своего места в жизни и внутренней позиции; формировании мировоззрения и его влияния на познавательную деятельность; самосознания и морального сознания.Методический материал:ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ. Многие физические законы, которым подчиняются те или иные явления, записываются в виде математического уравнения, выражающего определенную зависимость между какими-то величинами. Часто речь идет о соотношении между величинами, изменяющимися с течением времени, например экономичность двигателя, измеряемая расстоянием, которое автомашина может проехать на одном литре горючего, зависит от скорости движения автомашины. Соответствующее уравнение содержит одну или несколько функций и их производных и называется дифференциальным уравнением. (Темп изменения расстояния со временем определяется скоростью; следовательно, скорость – производная от расстояния; аналогично, ускорение – производная от скорости, так как ускорение задает темп изменения скорости со временем.) Большое значение, которое имеют дифференциальные уравнения для математики и особенно для ее приложений, объясняются тем, что к решению таких уравнений сводится исследование многих физических и технических задач. Дифференциальные уравнения играют существенную роль и в других науках, таких, как биология, экономика и электротехника; в действительности, они возникают везде, где есть необходимость количественного (числового) описания явлений (коль скоро окружающий мир изменяется во времени, а условия изменяются от одного места к другому).

Дифференциальные уравнения являются одним из самых мощных средств математического решения практических задач. Особенно широко они используются для решения задач естественнонаучного цикла: механики, физики, химии и биологии. Во многих задачах геометрической оптики, геодезии, картографии и других областей естествознания возникает необходимость нахождения кривых по заданным свойствам проведенных к ним касательным. Обычно такие геометрические задачи решаются так же с помощью дифференциальных уравнений.