Что такое последовательность.
Последовательность – функция натурального аргумента (f(n)) где n  N. (f(n))= х1,х2,…,хn,…
N. (f(n))= х1,х2,…,хn,…
Если каждому натуральному числу n поставлено в соответствие одно определенное значение хn, то говорят, что задана последовательность с общим членом хn, пишут (хn).
Послед-ть (хn) наз. возрастающей, если большему номеру соответствует больший член послед-ти, т.е xn+1>xn. Пр: (n)=1,2,3,…,n,…; (n2)=1,4,9,…, n2,…
Послед-ть (хn) наз. убывающей, если большему номеру соответствует меньший член послед-ти, т.е. xn+1<xn. Пр: (1/n)=1,1/2,1/3,…,1/n,…
Послед-ть (хn) наз. стационарной, если все ее члены одинаковые. Пр: (5)=5,5,5,…,5,…
(хn) наз. колеблющейся, если ее члены колеблются около какого-нибудь числа. пр: 1,-1,2,-2,…,n,-n,…
Числовая послед-ть (хn) наз. ограниченной, если найдётся такое положительное число с, что для всех n-членов послед-ти выполняется неравенство: /xn/ 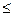 c.
c.
Числовая послед-ть (хn) наз. ограниченной сверху, если найдётся такое число М, что для всех членов послед-ти выполняется неравенство: xn 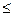 М.
М.
Пр: (-n)=-1,-2,…,-n,… sup 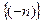 =-1
=-1
Числовая послед-ть (хn) наз. ограниченной снизу, если найдётся такое число m, что для всех членов послед-ти выполняется неравенство: xn≥m.
Пр: (n)=1,2,3,…,n,… inf 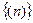 =1
=1
Числовая послед-ть (хn) наз. ограниченной, если сущ-ют m,M, что для всех членов послед-ти : m 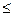 xn
xn 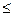 М.
М.
Пр: (1/n)=1,1/2,…,1/n,… sup 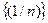 =1 inf
=1 inf 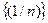 =0
=0
Число а наз. пределом числовой послед-ти с общим членом хn, если для любого положительного, наперёд заданного и сколь угодно малого числа 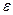 , найдется такое натуральное число n0, что для всех членов послед-ти с номерами n>n0 выполняется неравенство:
, найдется такое натуральное число n0, что для всех членов послед-ти с номерами n>n0 выполняется неравенство: 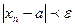 , т.е.
, т.е. 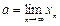
 Геометрический смысл числовой послед-ти:
Геометрический смысл числовой послед-ти:
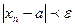

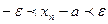

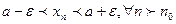
Геометрический смысл закл-ся в том, что внутри окрестности (а - 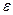 ; а +
; а + 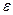 ) находится бесконечное число членов этой последовательности, а за ее пределами – конечное (х1,х2,…,хn)
) находится бесконечное число членов этой последовательности, а за ее пределами – конечное (х1,х2,…,хn)
Если число а явл-ся пределом числовой послед-ти, то говорят, что послед-ть сходится к а, а если предела не существует то посл-ть наз-ся расходящейся.
Пр: Доказать, что 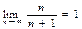
Выберем произвольную 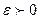 и составим модуль разности
и составим модуль разности 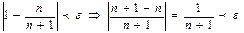
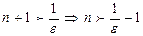 Мы нашли n0=
Мы нашли n0= 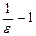 (целое), т.е
(целое), т.е 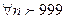 будет выполняться данное неравенство.
будет выполняться данное неравенство.
Послед-ть (αn) наз. бесконечно малой, если 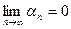 . Послед-ть (хn) наз. бесконечно большой, если
. Послед-ть (хn) наз. бесконечно большой, если 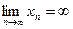 .
.
Т(о единственности предела числ. посл-ти): Если посл-ть (хn) имеет предел, то он единственный.
Док-во: (от противного) предположим, что посл-ть (хn) имеет два разных предела 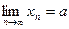 и
и 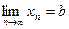 , a≠b, b>a. Т.к.
, a≠b, b>a. Т.к. 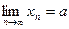 , то по опр.
, то по опр. 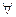 ε>0
ε>0 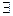 n1,
n1, 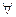 n>n1: |xn-a|<ε (1). Т.к.
n>n1: |xn-a|<ε (1). Т.к. 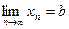 , то для выбр. ε>0
, то для выбр. ε>0 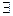 n2,
n2, 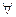 n>n2: |xn-b|<ε (2). Обозначим через n0=max{ n1; n2}, тогда для люб. n>n0: (1),(2). Составим разность b-a=|b-a|=|b-a+хn-хn |=|(хn–a)-(хn–b)| ≤| хn-a|+| хn-b|<ε+ε=2ε (|x
n>n2: |xn-b|<ε (2). Обозначим через n0=max{ n1; n2}, тогда для люб. n>n0: (1),(2). Составим разность b-a=|b-a|=|b-a+хn-хn |=|(хn–a)-(хn–b)| ≤| хn-a|+| хn-b|<ε+ε=2ε (|x 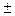 y|≤|x|
y|≤|x| 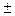 |y|)
|y|)
Т.о. b-a<2ε. Т.к.ε-произвольное, пусть 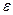 =
= 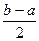 ,
,  b-a<2*
b-a<2* 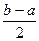 , b-a не< b-a
, b-a не< b-a  получили противоречие, оно говорит о том, что наше предположение неверно. Т.о.,
получили противоречие, оно говорит о том, что наше предположение неверно. Т.о., 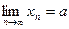 - единственный
- единственный
Т: Если 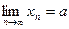 и
и 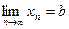 , то
, то
1)  ; 2)
; 2) 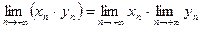
3) 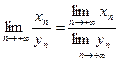 , если
, если 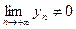 ;
;
4) 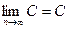 , где C=const; 5)
, где C=const; 5) 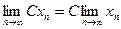 .
.
МЕТОДИКА 1.
Урок алгебры по теме "Арифметическая прогрессия" для 9 класса
Цели
Обучающие: - формировать понятие арифметической прогрессии, ознакомить учащихся с формулой нахождения n-го члена арифметической прогрессии;
- формировать навыки нахождения n-ого члена арифметической прогрессии; сформировать навыки использования формулы n-ого члена арифметической прогрессии при решении задач;
Развивающие: развивать умение делать выводы, обобщать и конкретизировать, логическое мышление, память; развивать навыки самоконтроля, самообразования; развивать умения: работать индивидуально, работать на результат.
Воспитательные: воспитать трудолюбие, усидчивость, самостоятельность, последовательность и аккуратность ведения записей, повысить интерес к изучаемому материалу.
Тип урока: Изложение нового материала
Структура урока:
- Сообщение темы, цели урока, мотивация учебной деятельности (орг.момент);
- Подготовительный этап через повторение и актуализацию опорных знаний;
- Ознакомление с новым материалом;
- Первичное осмысление;
- Постановка задания на дом;
- Итог.
Для создания положительной мотивации можно использовать историческую задачу. Ее не обязательно решать до конца, достаточно только с ее помощью ввести определение последовательности. А на этапе первичного закрепления вернуться к задаче и дорешать ее.
Историческая задача.
Задачи на прогрессии, дошедшие до нас из древности, были связаны с запросами хозяйственной жизни: распределение продуктов, деление наследства и др. Вот одна из них:
«Сто мер хлеба разделили между 5 людьми так, чтобы второй получил на столько же больше первого, на сколько третий получил больше второго, четвертый больше третьего и пятый больше четвертого. Кроме того, двое первых получили в 7 раз меньше трех остальных. Сколько нужно дать каждому?»
Решение.Обозначим долю первого заx , разница - y. Тогда:
Доля первого - x,
Доля второго - x+y,
Доля третьего - x+2y,
Доля четвертого - x+3y,
Доля пятого - x+4y.
Мы получили последовательность, которая называется арифметической пргрессией.
Рассмотрим определение арифметической прогрессии.
Арифметической прогрессией называется последовательность, каждый член которой, начиная со второго, равен предыдущему члену, сложенному с одним и тем же числом.
То есть, последовательность (an) – арифметическая прогрессия, если для любого натурального выполняется условие an +1 = an+d, где d - некоторое число.
Из определения арифметической прогрессии следует, что разность между любым ее членом, начиная со второго, и предыдущим членом равна, т.е. при любом натуральном верно равенство a n+1 – an= d.
Число d называется разностью арифметической прогрессии.
Чтобы задать арифметическую прогрессию, достаточно узнать ее первый член и разность. Например:
1.Если a1=1 и d=1, то получим арифметическую прогрессию
1; 2; 3; 4; 5;…, члены которой – последовательные натуральным числа.
2.Если a1=1 и d=2, то получим арифметическую прогрессию
1; 3; 5; 7; 9;…, которая является последовательностью положительных нечетных чисел.
3.Если a1=-2 и d=-2, то получим арифметическую прогрессию
-2; -4; -6; -8; -10;…, которая является последовательностью отрицательных четных чисел.
4.Если a1=7 и d=0, то имеем арифметическую прогрессию
7; 7; 7; 7; 7;…, все члены которой равны между собой.
Зная первый член и разность арифметической прогрессии, можно найти любой ее член, вычисляя последовательно второй, третий, четвертый и т.д. члены. Однако для нахождения члена прогрессии с большим номером такой способ неудобен. Постараемся отыскать способ, требующий меньшей вычислительной работы.
Зная, определение арифметической прогрессии можно вывести формулу n-го члена прогрессии
Исходя из определения арифметической прогрессии:
a2=a1+d,
a3=a2+d=(a1+d)+d=a1+2d,
a4=a3+d=(a1+2d)+d=a1+3d,
a5=a4+d=(a1+3d)+d=a1+4d.
Точно так же находим, что a6= a1+5d, и вообще, чтобы найти an, нужно к a1 прибавить (n-1)d, т.е.
an=a1+(n-1)d.
Получили формулы n-го члена арифметической прогрессии.
Формулу n-го члена арифметической прогрессии an=a1+(n-1)d можно записать иначе:
an=dn+(a1-d).
Отсюда ясно, что любая арифметическая прогрессия может быть задана формулой вида an=kn+b,
где k и b - некоторые числа.
Верно и обратное: последовательность (an), заданная формулой вида an=kn+b,
Дата добавления: 2021-12-14; просмотров: 384;











