Разложение в степенной ряд показательной функции
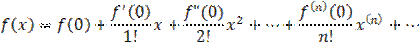
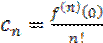
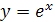
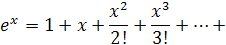
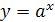
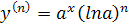
МЕТОДИКА 4.Формы, виды и средства контроля знаний и умений.
Формы контроля знаний и умений учащихся выделяются в соответствии с формами обучения:
- массовая (групповая, фронтальная);
- индивидуальная: фронтальный и индивидуальный опрос, контрольная работа, зачет, экзамен, диктант, сочинение.
Виды контроля:
1. По конечному результату:
- пошаговый контроль (за операциями);
- контроль, связанный с установлением определенных параметров деятельности.
2. По месту в процессе обучения:
- текущий (в ходе учения):
§ предварительный;
§ ежедневный;
§ периодический;
- итоговый по теме;
- итоговый по курсу обучения.
3. В новых педагогических технологиях рассматриваются следующие виды контроля усвоения знания и способов деятельности:
- входной;
- текущий, или промежуточный;
- итоговый.
Средства контроля: математический диктант, дидактические материалы, карточки, тесты, перфокарты, таблицы, опорные схемы, задания с печатной основой; кодоскоп, модели и приборы и т.д.
Задания для организации контроля на основе технологического подхода.
Входной контроль
Вариант №1
Инструкция: подчеркните ответ «да», если вы согласны с данным утверждением; если не согласны – «нет».
Текст задания.
- Показательное уравнение имеет вид: ах = b. (да, нет)
- Область значения функции y = ax – множество натуральных чисел. (да, нет)
- При любых действительных значениях x и y справедливо равенство: (ax)y = ax+y (да, нет)
- Функция y = ax возрастает при a > 1 и убывает при 0 < a < 1. (да, нет)
- Уравнение ах = b не имеет решений в случае b > 0 или b ≠ 0. (да, нет)
Эталон ответа: да, нет, нет, да, нет.
Вариант №2
Инструкция: заполните пропуски так, чтобы получилось верное утверждение.
Текст задания.
1. Функция, заданная формулой y = ax (где a > 0, a ≠ 1), называется показательной функцией с _________________ а.
2. Область определения показательной функции – множество ___________________ чисел.
3. Уравнение ах = b при любом положительном a, отличном от 1, и b > 0 имеет _______________________корень.
4. 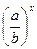 = …
= …
5. Показательная функция пересекает ось OY в точке с координатами _____.
Эталон ответа: 1 - основанием а; 2 – действительных; 3 – единственный; 4 - 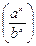 ; 5 - (0; 1).
; 5 - (0; 1).
Текущий контроль по теме «Показательные уравнения»
Решите уравнения:
-
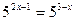
-
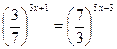
- 9х – 4 × 3х + 3 = 0;
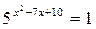
Итоговый контроль использован для проведения контрольной работы. (см. фрагмент урока)
Фрагмент урока на этапе контроля.
Тема: «Показательная функция».
Цели урока: Обучающая – выявить уровень овладения учащимися комплексом знаний и умений по теме «Показательная функция»;
Развивающая – развитие памяти, мышления;
Воспитательная – воспитывать интерес к математике.
Тип урока: урок проверки и контроля знаний и умений.
Структура урока
- Организационный момент (1 мин)
- Подготовка к контрольной работе (3 мин)
- Контрольная работа (35 мин)
IV.Подведение итогов урока (1 мин)
Ход урока
III. Контрольная работа.
Контрольная работа является итоговым контролем по теме «Показательная функция». Работа состоит из 2 вариантов. Задания записаны на доске.
| Вариант 1 | Вариант 2 | ||
| 1. | Постройте график функции: | ||
| y = 3x – 1 | y = 2 – 5x | ||
| 2. | Решите графически уравнение: | ||
| 2-х = 3х + 10 | 31-х = 2х – 1 | ||
| 3. | Решите уравнение: | ||
| 42х-6 – 17 · 4х-3 + 16 = 0 | 52х+10 – 6 · 5х+5 + 5 = 0 | ||
| 4. | Решите неравенство: | ||
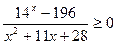
| 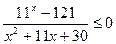
| ||
| 5. | Решите систему уравнений: | ||
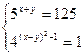
| 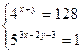
| ||
| 6. | Решите уравнение: | ||
| 2×4х - 3×10х - 5×25х = 0 | 4×9х + 12х - 3×16х = 0 | ||
Билет № 5. «Логарифмическая функция».
Пусть даны два числовых мн-ва X и У, и задано некоторое отобр-ие f. Если каждому элементу 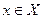 соответствует единственное значение
соответствует единственное значение 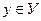 и при этом каждому значению у поставлено в соответствие единственное зн-ие х, то говорят, что между мн-вами Х и У установлено ВОС, кот-ое и наз-ся функцией.
и при этом каждому значению у поставлено в соответствие единственное зн-ие х, то говорят, что между мн-вами Х и У установлено ВОС, кот-ое и наз-ся функцией.
Ф-ция, заданная формулой у= 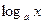 (a>0,a≠1, x>0), называется логарифмической ф-цией с основанием а.
(a>0,a≠1, x>0), называется логарифмической ф-цией с основанием а.
Основные св-ва логарифмической ф-ции:
10.Обл. определения – множество R+ положительных чисел. (0; +∞)
20. Обл. значений – мн-во всех действительных чисел.(-∞; +∞)
30. При a>1ф-ция возрастает на всей обл. определения; при 0<a<1 ф-ция убывает.
Док-во:
Рассмотрим, a>1 - ф-ция возрастает. Пусть х1 и х2 – произвольные положительные числа и х1 < х2. Надо доказать, что 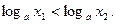 Предположим противное, что
Предположим противное, что 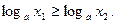 (*) Т.к. показательная ф-ция у=ах возрастает при a>1, то из неравенства (*) →
(*) Т.к. показательная ф-ция у=ах возрастает при a>1, то из неравенства (*) → 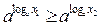 (**) , но по опр. логарифма
(**) , но по опр. логарифма 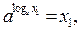
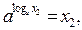 т.е. неравенство (**) означает, что х1 ≥ х2, а это противоречит предположению. Аналогично для убывающей.
т.е. неравенство (**) означает, что х1 ≥ х2, а это противоречит предположению. Аналогично для убывающей.
40. График лог. ф-ции проходит ч/з точку (1; 0).
у= 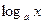 , a>1 у=
, a>1 у= 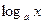 , 0<a<1
, 0<a<1
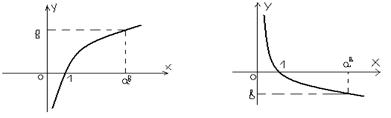
50.Знакопостоянство: если a>1, то у>0, х  (1; +∞) и у<0, x
(1; +∞) и у<0, x  (0; 1);
(0; 1);
если 0<a<1, то у>0, х  (0; 1) и у<0, x
(0; 1) и у<0, x  (1; +∞).
(1; +∞).
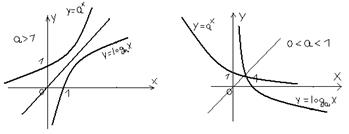
60 . Логарифмическая ф-ция у= 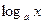 и показательная ф-ция у=ах , где a>0,a≠1, взаимно обратны. Их графики, имеющие одинаковое основание, симметричны относительно прямой у=х.
и показательная ф-ция у=ах , где a>0,a≠1, взаимно обратны. Их графики, имеющие одинаковое основание, симметричны относительно прямой у=х.
Основные св-ва логарифмов:
10. 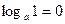
20. 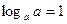
30. 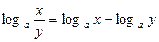
40. 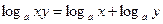
Док-во: (логарифм произведения равен сумме логарифмов)
Воспользуемся основным лог. тождеством: 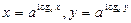 . Перемножая почленно эти равенства, получаем:
. Перемножая почленно эти равенства, получаем: 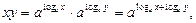 следовательно, по опр. логарифма
следовательно, по опр. логарифма 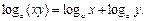
50. 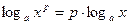
60. 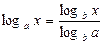 - формула перехода от одного основания к другому
- формула перехода от одного основания к другому
70. 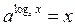 (b>0, a>0, a≠1)- основное лог. тождество.
(b>0, a>0, a≠1)- основное лог. тождество.
Логарифмическая ф-ция непрерывна и является дифференцируемой, т.е. её можно разложить в степенной ряд. Т.к. ф-ция 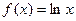 непрерывна в точке х=0 и её произведения в этой точке не существует, то рассмотрим ф-цию
непрерывна в точке х=0 и её произведения в этой точке не существует, то рассмотрим ф-цию 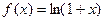 . Рассмотрим ряд Тейлора:
. Рассмотрим ряд Тейлора: 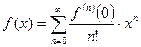 , это частный случай, когда х0=0 (ряд Макларена).
, это частный случай, когда х0=0 (ряд Макларена).
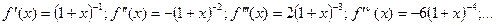
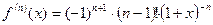 ;
; 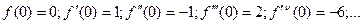
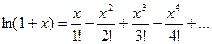 →
→ 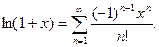
МЕТОДИКА 5. Методы мотивации изучения темы:
Необходимое условие для создания у учащихся интереса к содержанию обучения и к самой учебной деятельности — возможность проявить в учении умственную самостоятельность и инициативность. Чем активнее методы обучения, тем легче заинтересовать ими учащихся. Основное средство воспитания устойчивого интереса к учению — использование таких вопросов и заданий, решение которых требует от учащихся активной поисковой деятельности.
•Большую роль в формировании интереса к учению играет создание проблемной ситуации, столкновение учащихся с трудностью, которую они не могут разрешить при помощи имеющегося у них запаса знаний; сталкиваясь с трудностью, они убеждаются в необходимости получения новых знаний или применения старых в новой ситуации.. Интересна только та работа, которая требует постоянного напряжения. Легкий материал, не требующий умственного напряжения, не вызывает интереса. Преодоление трудностей в учебной деятельности — важнейшее условие возникновения интереса к ней. Трудность учебного материала и учебной задачи приводит к повышению интереса только тогда, когда эта трудность посильна, преодолима, в противном случае интерес быстро падает.
Учебный материал и приемы учебной работы должны быть достаточно (но не чрезмерно) разнообразны. Разнообразие обеспечивается не только столкновением учащихся с различными объектами в ходе обучения, но и тем, что в одном и том же объекте можно открывать новые стороны. Один из приемов возбуждения у учащихся познавательного интереса — «отстранение», т. e. показ учащимся нового, неожиданного, важного в привычном и обыденном. Новизна материала — важнейшая предпосылка возникновения интереса к нему. Однако познание нового должно опираться на уже имеющиеся у школьника знания. Использование прежде усвоенных знаний — одно из основных условий появления интереса. Существенный фактор возникновения интереса к учебному материалу - его эмоциональная окраска, живое слово учителя.
Эти положения, сформулированные С. М. Бондаренко, могут служит определенной программой организации учебного процесса, специально направленной на формирование интереса.
Дата добавления: 2021-12-14; просмотров: 409;











