МЕТОДИКА 2. «Понятие функции и способы задания функции»

Основные понятия темы: независимая и зависимая переменные, функция, область определения, область значений ф-ии, графики ф-ии.

Основные предложения темы:

- свойства функции (область определения, область значения, монотонность, периодичность, четность, нечетность, нули функции, промежутки знакопостоянства, экстремумы, непрерывность).

- способы задания функции (аналитический, табличный, графический, описание).

Фрагмент урока: «Понятие ф-ии» 7 класс

Тип урока: изучения нового материала

Цели:

Обучающие: - изучить основные функциональные понятия;

Развивающие: - развитие операционное мышление: умение анализировать, сравнивать, обобщать;

- развитие мировоззрения, речи, памяти;

Воспитательные:- воспитание интереса к математике;

- эстетическое воспитание.

Содержание урока:

1. Организационный момент (2-3 мин)

2. Актуализация знаний (6-7 мин)

3. Изучение нового материала (13-14 мин)

4. Усвоение нового материала (17-18 мин)

5. Домашнее задание (2-3 мин)

6. Итоги урока (2-3 мин)

Мотивация к изучению темы: «Понятие функции».

В зависимости от возрастных особенностей выделяют следующие методы мотивации: 1. проблемный способ изложения материала, 2. эмоциональный характер, 3. связь с практикой, с жизнью, 4. связь с прошлым материалом, 5. научно-факторная содержательность материала, 6. коллективная работа.

С учетом возрастных особенностей учащихся воспользуемся одним из методов мотивации – связь с жизнью – и подведем их к понятию функция, показав зависимость одной величины от другой, решив следующие задачи.

Задача 1. Из пункта А в пункт В отправился пешеход. Траектория пути изображена на графике. Расстояние от пункта А до пункта В 20 верст. Сколько верст прошел пешеход спустя 2 часа, 4 часа, 8 часов, 18 часов.

(для наглядности используется плакат с изображением графика зависимости)

Задача 2. На окраине леса шириной 100м запыленность воздуха составляет 65% от запыленности на открытом месте, на расстоянии 400м от края леса она снижается до 38%, 1000м – до 25%, 3км – до 5%. Постройте график зависимости уменьшения запыленности по мере удаления в лес.

Рис.1

Таким образом, ребята, зависимость переменной y от переменной x называется функцией, если каждому значению x соответствует единственное значение у

Билет № 3. «Дифференциальные уравнения».

Уравнение, содержащее независимую переменную x, функцию у и ее производную у', (не разрешимое) наз. дифференциальным уравнение I порядка (д/у) и обозначается: .

Интеграломдиф-го урав-яназ. соотношение, связывающее независимые переменные и искомую ф-цию, т.е. - интеграл диф-го урав-я - решение.

Условие при наз. начальным условием. (или , или )

Общим решением д/у I порядка наз. ф-ция , где с- произвольная постоянная, удовлетворяющая двум условиям:

1) она удовлетворяет данному д/у при любом конкретном значении с;

2) каково бы ни было начальное условие можно найти такое значение , что ф-ция б/т удовлетворять начальным условиям.

Д/у устанавливает связь (зависимость) между координатами точки (х;y) и угловым коэффициентом y^' касательной к интегральной кривой, проходящей через эту точку. Следовательно, д/у y'=ƒ(х;y) дает совокупность направлений (семейство кривых) на плоскости Охy. Таково геометрическое истолкование д/у I порядка

Частным решением д/уI порядка наз. любая ф-ция , которая получается из общего решения при конкретном значении произвольной постоянной .

Т(о существовании и единственности решения д/у I порядка): Если в д/у правая часть и частная производная явл-ся непрерывной в D, содержащую искомую (.)М(х₀,у₀) D, то 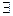, и при том единственное решение этого урав-я , которое удовлетворяет начальному условию: при .

Виды уравнений:

1) Уравнения с разделёнными переменными. Уравнения вида P(x) dx + Q(y) dy = 0.

∫P(x) dx +∫Q(y) dy = c- общий интеграл (общее решение) этого уравнения.

Пр: - уравнение с разделяющимися коэффициентами

- общий интеграл.

С точки зрения геометрии получим мн-во окружностей.

2) Уравнения с разделяющимися переменными. Уравнение вида

, общий интеграл.

Пр:

При такой форме записи общего интеграла решение y = 1 потеряно. Можно преобразовать общее решение к виду, который содержит это решение. Переобозначим постоянную C как ln|C₁|: Вернёмся к обозначению постоянной интегрирования C; общее решение содержит частное решение y = 1 при C = 0.