Закрепление материала
Изучив новый материал его необходимо закрепить
Задача 1. Проверить, какие из следующих конечных последовательностей являются арифметическими прогрессиями, и найти их а1 и d.
а) 1, 4, 7, 10; б) 1, 4, 15, 18; в) 1, -2, -5, -6; г) 1, -1, -3, -5.
Ответ: а, г.
Задача 2. В арифметической прогрессии (an), известно, что a1=2 и a11=-11. Найти разность арифметической прогрессии d.
Ответ: d=-1,3.
Задача 3. Выписать первые пять членов арифметической прогрессии, у которой а1=3, d=2.
Ответ: 3, 5, 7, 9, 11.
Задача 4. Является ли число 22,5 членом арифметической прогрессии (an): 6,8; 8; ..?
Ответ: число 22,5 не является членом данной арифметической прогрессии.
Задача 5. Курс воздушных ванн начинают с 15 мин. в первый день и увеличивают время этой процедуры в каждый следующий день на 10 минут. Сколько дней следует принимать ванны в указанном режиме, чтобы достичь их максимальной продолжительности 1 час 45 минут?
Ответ:10 дней следует принимать ванны
Билет № 2.«Функция».
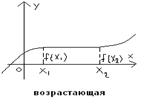 Пусть даны два числовых мн-ва X и У, и задано некоторое отобр-ие f. Если каждому элементу
Пусть даны два числовых мн-ва X и У, и задано некоторое отобр-ие f. Если каждому элементу 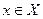 соответствует единственное значение
соответствует единственное значение 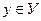 и при этом каждому значению у поставлено в соответствие единственное зн-ие х, то говорят, что между мн-вами Х и У установлено ВОС, кот-ое и наз-ся функцией.
и при этом каждому значению у поставлено в соответствие единственное зн-ие х, то говорят, что между мн-вами Х и У установлено ВОС, кот-ое и наз-ся функцией.
Х – область опр-ия ф-ции.
у=f(x) возраст., если большему значению аргумента соотв-ет большее зн-ие ф-ции
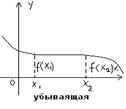 у=f(x) убыв., если большему значению аргумента соотв-ет меньшее значение ф-ции
у=f(x) убыв., если большему значению аргумента соотв-ет меньшее значение ф-ции
у=f(x)-периодическая с периодом Т, если f(x+Т)=f(x)
у=f(x)-четная на симметричном отн-но т.0 (начала координат) промежутке, если f(-x)=f(x).
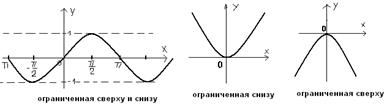 у=f(x)-нечетная на симметричном отн-но т.0 (начала координат) промежутке, если f(-x)=-f(x).
у=f(x)-нечетная на симметричном отн-но т.0 (начала координат) промежутке, если f(-x)=-f(x).
у=f(x)-ограничена сверху, если 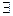 М,
М, 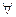 х
х  Х: f(x)≤M
Х: f(x)≤M
у=f(x)-ограничена снизу, если 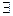 m,
m, 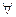 х
х  Х: f(x)≥m
Х: f(x)≥m
у=f(x)-ограниченная, если 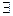 К>0,
К>0, 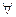 x
x  Х:| f(x)|≤К
Х:| f(x)|≤К
у=f(x)-явная
у=F(x,y)-неявная
Число а наз. пределом ф-ции f(x) в точке х0, если 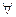 ε>0, найдётся δ>0 зависящее от ε, то для
ε>0, найдётся δ>0 зависящее от ε, то для 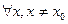 удовлетворяющих неравенству
удовлетворяющих неравенству 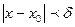 :
: 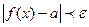 , т.е.
, т.е. 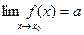
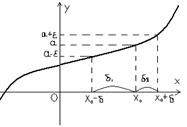 Геометрический смысл:
Геометрический смысл: 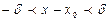
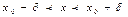
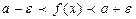
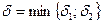 , т.е.
, т.е. 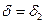
Когда х попадает в δ-окрестность точки х0, х 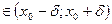 соответствующее значение ф-ции попадает в ε-окрестность точки а
соответствующее значение ф-ции попадает в ε-окрестность точки а 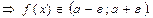
Т: Пусть 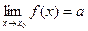 и
и 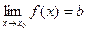 , то
, то
1) 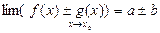 , 2)
, 2) 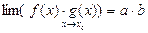
3) 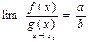 ,
, 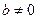 ,4)
,4) 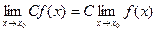 ,5)
,5) 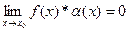
Док-во: 1) На основании теоремы, что если ф-ция имеет своим пределом число а, то она может быть представлена в виде суммы своего предела и бесконечно малой f(x)=a+ α(х) при х→х0, т.е. f(x)= a+α(х), где α(x)-бесконечно малая при х→х0, а g(x)=a+β(х), где β(х)-бесконечно малая при х→х0  f(x)+g(x)=(a+b)+ (α(х)+β(х)), то по обратной теореме: если ф-ция м/б представлена в виде суммы числа и бесконечно малого, то это число явл-ся пределом для данной ф-ции.
f(x)+g(x)=(a+b)+ (α(х)+β(х)), то по обратной теореме: если ф-ция м/б представлена в виде суммы числа и бесконечно малого, то это число явл-ся пределом для данной ф-ции.
2) Тоже самое, только : f(x)*g(x)=(a*b)+ (b*α(х) + a*β(х) + α(х)*β(х)), то по обр. теореме доказано.
3) 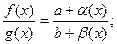 α(x),β(х)-бесконечно малые, при х→х0.
α(x),β(х)-бесконечно малые, при х→х0. 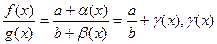 -бесконечно малое, при х→х0
-бесконечно малое, при х→х0 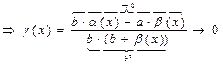
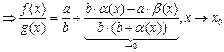 , то по обр. теореме доказано.
, то по обр. теореме доказано.
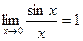 - 1-ый зам. предел
- 1-ый зам. предел 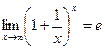 - 2-ой зам. предел
- 2-ой зам. предел
Пусть ф-ция f(x) определена на мн-ве Х, а (.)х0  Х, то ф-ция f(x) непрерывна в (.)х0:
Х, то ф-ция f(x) непрерывна в (.)х0: 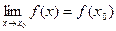
(по Коши) Ф-ция f(x) непрерывна в (.)х0 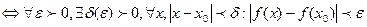 .
.
(по Гейне) Ф-ция f(x) непрерывна в (.)х0, если какую бы послед-ть различных точек х1,х2,…,хn,… сходящихся к х0 не взять, послед-ть соответствующих значений ф-ций f(х1),f(х2),…,f(хn),… сходится к f(х0).
(на яз.приращ) Ф-ция f(x) непрерывна в (.)х0, если бесконечно малому приращению аргумента соответствует бесконечно малое приращению ф-ции.
Точка х0 наз. точкой разрыва ф-ции f(x), если в ней нарушено какое-либо условие непрерывности, а именно:
1)  f(x) м/б неопределенна в (.)х0 (не существовать);
f(x) м/б неопределенна в (.)х0 (не существовать);
2) м/б не существует предел ф-ции f(x) при х→х0;
3) 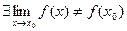
Точка х0 наз. точкой устранимого разрыва, если предел в этой точке существует но не равен f(x0)- значению ф-ции или предел в этой точке существует, но сама ф-ция в (.)х0 не определена.
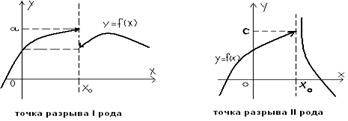
Точка х0 наз. точкой разрыва I рода, если односторонние пределы существуют, но не равны между собой.
Точка х0 наз. точкой разрыва II рода, если хотя бы один из односторонних пределов не существуют или равен 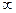 .
.
Т(1-ая Т.Больцано-Коши): Если ф-ция у=f(x) непрерывна на отрезке [a,b] и на концах отрезка принимает значения разных знаков, то найдётся хотя бы одна (.)с є [a,b], в которой ф-ция обращается в 0, т.е. f(с)=0.
Т(2-ая Т. Б-К): Если ф-ция у=f(x) непрерывна на отрезке [a,b] и принимает на его концах разные значения, то какое бы число М мы не взяли, лежащее между f(a) и f(b), то внутри отрезка [a,b] найдётся такая (.)С, в которой f(С)=М.
Док-во:
Пусть f(a)<f(b), f(a)<М<f(b).
Рассм. φ(х)=f(x)-M и найдем ее значение на концах отрезка: φ(a)=f(a)-M<0; φ(b)=f(b)-M>0; φ(x)-непр. как разность непр. ф-ции и константы (1Т.Б-К). Значит внутри отрезка [a,b] найдется такая т.С, в которой ф-ция
φ(с)=0  f(c)-M=0
f(c)-M=0  f(c)=M
f(c)=M
Т(1-ая Т.Вейерштрасса): Если ф-ция у=f(x) непрерывна на отрезке [a,b], то она на нем ограничена .
Т(2-ая Т.В): Если ф-ция у=f(x) непрерывна на отрезке [a,b], то она достигает на этом отрезке своих наибольших и наименьших значений.
Дата добавления: 2021-12-14; просмотров: 302;











