Деформация кручения брусьев прямоугольного сечения

Испытания стержней некруглого сечения на кручение показывают, что поперечные сечения таких стержней после деформации перестают быть плоскими. Это явление, связанное с выходом точек поперечного сечения из плоскости, называется депланацией сечения. Когда депланация всех поперечных сечений одинакова, она считается свободной и не приводит к появлению нормальных напряжений в продольных волокнах. В противном случае депланация является стесненной и сопровождается появлением нормальных напряжений в продольных волокнах. В данной части курса мы не будем учитывать влияние стесненности депланации, т.е. будем рассматривать свободное кручение стержней.

Распределение касательных напряжений при кручении стержней прямоугольного сечения более сложное, чем стержней круглого сечения из-за наличия депланации. Эта задача была впервые решена Сен-Венаном в теории упругости. На рис. 6.5 показана картина распределения касательных напряжений в поперечном сечении прямоугольной формы. Величина максимального касательного напряжения определяется по формуле:

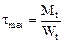. (6.16)

Здесь W_t = ahb² – момент сопротивления сечения при кручении.

Дифференциальное уравнение для углов закручивания аналогично уравнению для стержня круглого сечения и имеет вид:

,

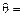
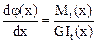где I_t = bhb³ – момент инерции при кручении стержня прямоугольного сечения. Величины a, b, g называют коэффициентами Сен-Венана, их используют при расчете брусьев прямоугольного сечения на кручение. Данные коэффициенты зависят от соотношения h/b и приведены в табл. 6.1.

Таблица 6.1

h/b	1,0	1,5	1,75	2,0	2,5	3,0	4,0	6,0	8,0	10,0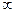
α	0,208	0,231	0,239	0,246	0,256	0,267	0,282	0,299	0,307	0,313	0,333
β	0,141	0,196	0,214	0,229	0,249	0,263	0,281	0,299	0,307	0,313	0,333
γ	1,0	0,859	0,820	0,795	0,766	0,753	0,745	0,743	0,742	0,742	0,743

Условия прочности и жесткости записываются аналогично (6.4), (6.15), (6.15)'.

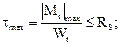(6.17)

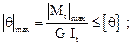(6.18)

. (6.19)

Здесь a – полный угол закручивания сечения по отношению к защемленному сечению, определяется по тем же формулам, что и для круглого сечения, заменяя в них I_r на I_t.

Подбор сечения выполняется в том же порядке, как и для стержней круглого сечения.

ПРИМЕР 6.2

Для бруса, изображенного на рис. 6.6требуется:

– построить эпюру крутящих моментов;

– из условия прочности при кручении подобрать размеры прямоугольного поперечного сечения;

– построить эпюру углов закручивания сечений при следующих исходных данных:

М₁ = 2,1 кН м; М₂ = 1,2 кН м; М₃ = 2,7 кН м;

h/b = 2; R_S = 70 МПа; G = 8 10⁴ МПа.

РЕШЕНИЕ

1. Построим эпюры крутящих моментов М_t. Рассматривая правую отсеченную часть стержня для каждого грузового участка получим:

М = М₁ = 2,1 кН м;

М 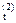= М₁ – М₂ = 2,1 – 1,2 = 0,9 кН м;

М 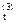= М₁ – М₂ – М₃ = 2,1 – 1,2 – 2,7 = –1,8 кН м.

Эпюра М_t показана на рис. 6.6б.

2. Определим необходимые размеры сечения, из условия прочности (6.17):

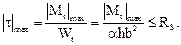
Для отношения 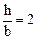из табл. 6.1 находим a = 0,246.

При h = 2b и при условии 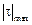= R_S, 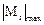= 2,1 кН×м получим 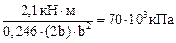. Отсюда находим:

b = 3,935 10^–2 м.

После округления окончательно принимаем:

b = 4 см, h = 2b = 2 4 = 8 см.

Проверим прочность подобранного сечения:

W_t = = 0,246 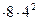= 31,5 см³;

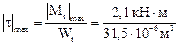= 66,67 10³ кПа < R_S = 70 10³ кПа.

3. Построим эпюру полных углов закручивания.

Предварительно определим момент инерции при кручении и значение жесткости поперечного сечения при кручении GI_t:

I_t = bhb³ = 0,229×8×4³ = 117,25 см⁴ = 117,25 10^–8 м⁴

(при h/b = 2 b = 0,229 (табл. 6.1));

G = 0,8 10⁵ МПа = 0,8 10⁸ кПа.

GI_t = 0,8 10⁸ кН/м² × 117,25 × 10^–8 м⁴ = 93,8 кН×м².

Определим полные углы закручивания сечений А, В, С, D как сумму углов взаимного закручивания концов участков, заключенных между рассматриваемым и защемленным сечениями.

a_А = 0 (здесь стержень защемлен);

a_В = a_А + j₃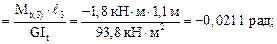

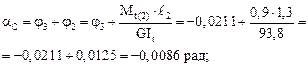
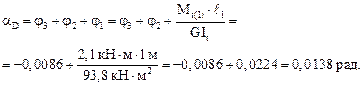
Эпюра полных углов закручивания a показана на рис. 6.6в.