Определение напряжений и расчеты на прочность при деформации кручения брусьев круглого сечения

Кручением называется такой вид деформации стержня, при котором в его поперечных сечениях возникают только крутящие моменты, другие внутренние силовые факторы – продольная сила, изгибающие моменты и поперечные силы – равны нулю.

Теория кручения брусьев, имеющих круглое сплошное или кольцевое поперечное сечение, основана на следующих положениях:

1. Поперечные сечения бруса, плоские и нормальные к его оси до деформации, остаются плоскими и нормальными к ней и после деформации (гипотеза плоских сечений), они лишь поворачиваются на некоторые углы вокруг этой оси.

2. Радиусы поперечных сечений не искривляются и сохраняют свою длину.

3. Расстояния (вдоль оси бруса) между поперечными сечениями не изменяются.

В поперечном сечении бруса возникают только касательные напряжения от крутящего момента, определяемые по формуле (6.1). Их направление в каждой точке перпендикулярно радиусу, соединяющему эту точку с центром сечения (рис. 6.1). В центре (при ρ = 0) касательные напряжения равны нулю; в точках же, расположенных в непосредственной близости от внешней поверхности бруса, они наибольшие.

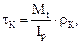(6.1)

где 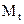– крутящий момент в рассматриваемом сечении; 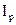– полярный момент инерции круглого поперечного сечения; r_К – расстояние от центра тяжести сечения до рассматриваемой точки К (рис. 6.1).

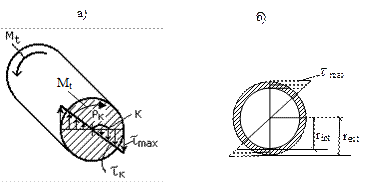
Рис. 6.1

Эпюры 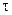, построенные по формуле (6.1) для круглого сплошного и кольцевого сечений, представлены на рис. 6.1а, б.

Наибольшие касательные напряжения в поперечных сечениях определяются по формуле:

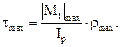(6.2)

Введем следующее обозначение:

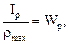(6.3)

где 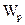– называется полярным моментом сопротивления поперечного сечения (см³, м³); 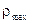– расстояние от центра тяжести до наиболее удаленной точки сечения, оно равняется радиусу круга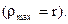

Условие прочности при кручении запишется:

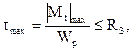(6.4)

где R_S – расчетное сопротивление материала при сдвиге.

Используя условие прочности (6.4), можно решать следующие задачи на кручение:

1. Проверочная задача, т.е. проверка прочности. Подставляя в формулу (6.4) величины 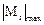из эпюры крутящих моментов и W_r, определенную по формуле (6.3), проверяем, выполняется ли условие прочности.

2. Проектная задача, т.е. подбор сечения. В этом случае из условия прочности (6.4), предполагая, что 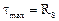, определяется значение требуемого полярного момента сопротивления:

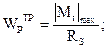(6.5)

Затем значение 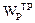приравнивается выражению 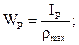т.е.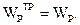

Из этого равенства определяется неизвестный диаметр стержня.

Ниже приведены формулы для определения полярных моментов сопротивления для стержней круглого поперечного сечений:

а) сплошное круглое сечение (рис. 6.2а):

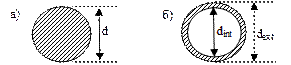
Рис. 6.2

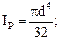(6.6)

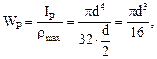(6.7)

здесь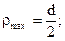

б) кольцевое сечение (рис. 6.2б):

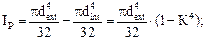(6.8)

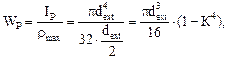(6.9)

Здесь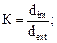

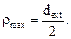
3. Определение допускаемого значения крутящего момента для стержня заданного диаметра и из заданного материала.

Из условия прочности (6.4), которое берем со знаком равенства, т.е. 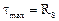, определяем значение допускаемого крутящего момента:

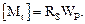(6.10)