Исследование объемного напряженного состояния
Как было показано ранее в п. 4.1, напряжения, действующие на гранях элементарного параллелепипеда, в общем случае напряженного состояния представляются в виде тензора напряжений (рис. 4.4а), как упоминалось:
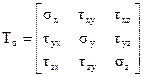 .
.
Тензор напряжений симметричен относительно главной диагонали, поскольку по закону парности касательных напряжений имеем:
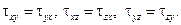
Рассмотрим определение главных напряжений и положения главных площадок в случае объемного напряженного состояния (все три главных напряжения не равны нулю) (рис. 4.4б).
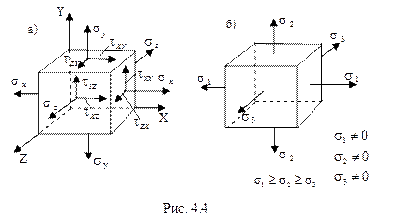
Предположим, что нам известно положение главной площадки, определяемой нормалью 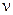 . Сечением, параллельным этой площадке, выделим из исходного параллелепипеда тетраэдр, изображенный на рис. 4.5б, и составим условия равновесия тетраэдра в виде суммы проекций действующих на него сил на оси координат. Введем обозначения для направляющих косинусов нормали
. Сечением, параллельным этой площадке, выделим из исходного параллелепипеда тетраэдр, изображенный на рис. 4.5б, и составим условия равновесия тетраэдра в виде суммы проекций действующих на него сил на оси координат. Введем обозначения для направляющих косинусов нормали 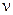 :
:
cos( 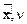 ) =
) = 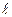 ; cos(
; cos( 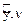 ) = m; cos(
) = m; cos( 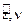 ) = n. (4.16)
) = n. (4.16)
Примем площадь наклонной грани тетраэдра dA = 1, тогда площади других граней будут: dAX = 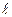 , dAy = m, dAZ = n.
, dAy = m, dAZ = n.
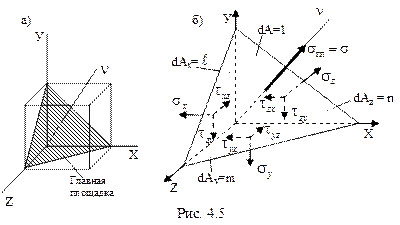
Единственное напряжение, действующее на главной площадке, обозначим 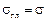 . Сумма проекций сил на ось Х запишется в виде:
. Сумма проекций сил на ось Х запишется в виде:
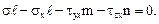
Аналогичные равенства будут для осей Y и Z. Все вместе они составят систему однородных уравнений относительно неизвестных косинусов 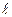 , m и n:
, m и n:
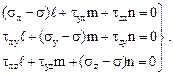 (4.17)
(4.17)
Так как между неизвестными существует зависимость
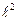 +m2+n2 = 1, (4.18)
+m2+n2 = 1, (4.18)
то одновременно они все не могут быть равны нулю. В этом случае (доказано в линейной алгебре) определитель однородной системы уравнений равен нулю, т.е.
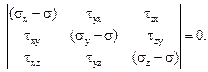 (4.19)
(4.19)
Раскрыв определитель, получим кубическое уравнение
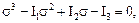 (4.20)
(4.20)
три корня которого и будут значениями трех главных напряжений в рассматриваемой точке.
Коэффициенты уравнения (4.20) получаются при раскрытии определителя (4.19) и имеют следующий вид:
I1 = 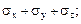
I2 = 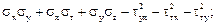 (4.21)
(4.21)
I3 = 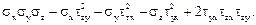
Эти коэффициенты не зависят от выбора осей координат, поскольку при любых исходных площадках уравнение (4.20) должно давать одни и те же корни 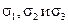 – главные напряжения в точке. Они называются первым, вторым и третьим инвариантами напряженного состояния (тензора напряжений).
– главные напряжения в точке. Они называются первым, вторым и третьим инвариантами напряженного состояния (тензора напряжений).
Для определения направляющих косинусов 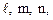 соответствующих одной из трех главных площадок, значение главного напряжения на этой площадке надо подставить в (4.17) вместо
соответствующих одной из трех главных площадок, значение главного напряжения на этой площадке надо подставить в (4.17) вместо 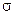 . Совместное решение уравнений (4.17) и (4.18) и даст искомые значения направляющих косинусов
. Совместное решение уравнений (4.17) и (4.18) и даст искомые значения направляющих косинусов 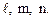
Дата добавления: 2021-12-14; просмотров: 567;











