Основные положения и определения

Как было показано в главе 3, при изучении центрального растяжения и сжатия прямых стержней, сопротивление стержня пропорционально площади поперечного сечения А: чем больше площадь поперечного сечения, тем меньше напряжение и деформация при одинаковом значении продольной силы.

Площадь является простейшей геометрической характеристикой поперечного сечения.

При расчетах на изгиб, кручение, сложное сопротивление, а также при расчете сжатых стержней на устойчивость используются более сложные геометрические характеристики поперечных сечений:

– статический момент площади;

– осевой (экваториальный) момент инерции;

– полярный момент инерции;

– центробежный момент инерции сечения.

Дадим определения этим геометрическим характеристикам для сечения произвольной формы (рис. 5.1).

Статическим моментом площади относительно некоторой оси называется взятый по всей его площади интеграл от произведения площади элементарного участка dA на расстояние от его центра тяжести до рассматриваемой оси.

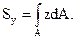(5.1)

Статические моменты выражаются в см³ и м³.

Статический момент площади составной фигуры относительно какой-либо оси равен сумме статических моментов площадей отдельных фигур относительно этой же оси.

В случае сложного сечения, состоящего из n частей, для которых известны площади и положения центров тяжести, выражение (5.1) примет вид:

(5.2)

где 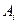– площадь i-й части сложного сечения; 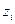и – расстояния от центров тяжести i-й отдельной части до осей Z и Y (рис. 5.2); n – число частей.

Статический момент площади может быть положительным, отрицательным или равным нулю. Он равняется нулю тогда, когда рассматриваемая ось проходит через центр тяжести площади сечения.

Из курса теоретической механики известно, что если известны площади и центры тяжести отдельных частей сложного сечения (рис. 5.2), то координаты его центра тяжести y_C и z_C относительно произвольно выбранной системы координат Y' и Z' определяются по следующим формулам:

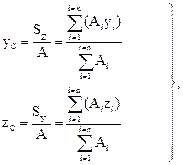(5.3)

Здесь – y_i и z_i – координаты центров тяжести отдельных частей относительно произвольно выбранной системы координат Y' и Z'; А_i – площади отдельных частей; n – количество отдельных частей.

Произвольные оси Y' и Z' рекомендуется выбирать так, чтобы сложное сечение находилось в положительной четверти, и чтобы одна или обе оси проходили бы через центр тяжести одной из простых фигур. Это упрощает вычисления (рис. 5.2).

Осевым (экваториальным) моментом инерции сечения относительно некоторой оси называется взятый по всей его площади А интеграл от произведения площади элементарного участка dA на квадрат расстояния от его центра тяжести до рассматриваемой оси:

(5.4)

Полярным моментом инерции сечения относительно некоторой точки (полюса) называется взятый по всей его площади А интеграл от произведения площади элементарного участка dA на квадрат расстояния от его центра тяжести до рассматриваемой точки (полюса):

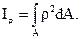(5.5)

Центробежным моментом инерции сечения относительно некоторых двух взаимно перпендикулярных осей называется взятый по всей его площади А интеграл от произведения площади элементарного участка dA на расстояния от его центра тяжести до рассматриваемых осей:

(5.6)

Моменты инерции измеряются в см⁴ и м⁴. Осевые и полярные моменты инерции всегда положительны. Центробежные моменты инерции могут быть положительными, отрицательными или равными нулю.

Центробежный момент инерции сечения относительно осей, из которых одна или обе совпадают с его осями симметрии, равен нулю.

Оси, относительно которых центробежный момент инерции равен нулю, называются главными осями. Осевые моменты инерции относительно таких осей принимают экстремальные значения и называются главными моментами инерции.

Центральные оси, относительно которых центробежный момент инерции равен нулю, называются главными центральными осями инерции.

Порядок определения положения главных осей и величин главных моментов инерции для сечений, не имеющих ни одной оси симметрии, будет рассмотрен дальше.

Осевой момент инерции сложного сечения относительно оси Z (или Y) равен сумме осевых моментов инерции составляющих его частей (простых фигур) относительно этой же оси.

Центробежный момент инерции сложного сечения относительно некоторых осей Z и Y равен сумме центробежных моментов инерции составляющих его частей (простых фигур) относительно этих же осей.

(5.7)

Если известны осевые и центробежный моменты инерции отдельной части сечения относительно центральных осей этой части, то моменты инерции относительно осей Z и Y, проходящих через центр тяжести всего сечения и параллельных центральным осям отдельной части, определяются по формулам:

(5.8)

Здесь: – моменты инерции отдельных частей относительно их центральных осей (собственные моменты инерции); – координаты центра тяжести i-й части относительно центральных осей всего сечения Z и Y. С учетом (5.7) и (5.8) можно получить формулы (5.9) для определения моментов инерции сложных сечений, состоящих из n простых частей (см. рис. 5.2).

Таким образом, для определения моментов инерции сложных сечений в первую очередь их необходимо разбить на простые части и определить моменты инерции простых фигур относительно собственных центральных осей:

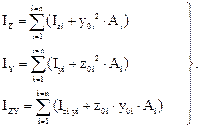(5.9)