Деформированное состояние в точке. Обобщенный закон Гука

Установим зависимость относительной линейной деформации от нормальных напряжений в случае объемного напряженного состояния.

Определим относительную продольную деформацию выделенного элемента (см. рис. 4.1б) в направлении главного напряжения σ₁, отдельно рассматривая влияние каждого из главных напряжений и складывая результаты в соответствии с принципом независимости действия сил:

.

Под действием напряжения σ₁ элемент в направлении этого напряжения на основании закона Гука получит относительное удлинение, равное 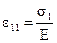. (Аналогично определятся относительные деформации по направлениям двух других главных напряжений: ; ).

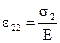В то же время по отношению к напряжениям σ₂ и σ₃, ребро элемента, параллельное σ₁, является поперечным размером, а потому под действием напряжений σ₂ и σ₃ элемент в направлении σ₁ испытывает относительные укорочения, равные:

, .

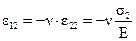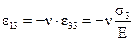Здесь 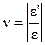– коэффициент поперечной деформации, называемый коэффициентом Пуассона; ε' – относительная поперечная деформация; ε – относительная продольная деформация.

Таким образом, полная относительная деформация элемента в направлении напряжения σ₁ выразится суммой:

.

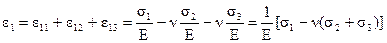Подобные же выражения получим и для деформаций в двух других направлениях. В результате имеем:

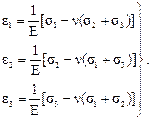(4.22)

Касательные напряжения не вызывают удлинений ребер выделенного параллелепипеда, а вызывают лишь изменения прямых углов между его гранями. Закон Гука в общем виде (рис. 4.1а) для объемного напряженного состояния запишется:

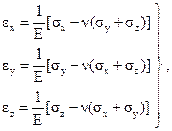
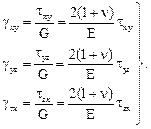(4.23)

В соотношениях (4.23) использована зависимость между тремя упругими постоянными материала – модулем упругости 1-го рода Е, коэффициентом Пуассона n и модулем упругости 2-го рода (модулем сдвига) G:

G = .

Формулы (4.23) показывают, что при изменении нормальных и касательных напряжений на всевозможных площадках, проходящих через заданную точку, соответственно изменяются относительные линейные деформации и углы сдвига граней выделенного элемента с бесконечно малыми размерами dx, dy, dz.

Совокупность линейных относительных деформаций и углов сдвига для всевозможных направлений осей, проведенных через заданную точку, называется деформированным состоянием в точке.

Деформации элемента в трех ортогональных плоскостях представим в виде таблицы

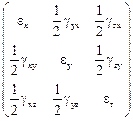
аналогичной тензору напряжений и называемой тензором деформаций.

Выражения (4.22) и (4.23), устанавливающие связь между деформациями и напряжениями в общем случае напряженного состояния, носят название обобщенного закона Гука. Они применимы при напряжениях, не превышающих предел пропорциональности материала и при малых деформациях.

С помощью формул (4.23) обобщенного закона Гука можно определять относительные деформации по любому заданному направлению, если предварительно определить нормальные напряжения вдоль указанного направления и двух других направлений, перпендикулярных заданному.

Относительные деформации ε₁, ε₂, ε₃ в направлениях, для которых отсутствуют углы сдвига, определяемые по формулам (4.22), называются главными деформациями.

Для главных направлений тензор деформаций получит вид:

.