Исследование плоского напряженного состояния

Как было указано выше, если одно из главных напряжений равно нулю, то объемное напряженное состояние исключается. Однако, чтобы точно сказать, плоское или одноосное напряженное состояние имеет место в данной точке, необходимо определить два других главных напряжения.

Вырежем параллелепипед с бесконечно малыми размерами сторон dx, dy, dz так, чтобы на одной из трех взаимно перпендикулярных площадок отсутствовали напряжения. Это будет означать, что одно главное напряжение равно нулю. В этом случае, как указывалось ранее, не будет объемного напряженного состояния. Такие элементы можно вырезать из стенки изгибаемых балок, стеновых панелей и т.п., когда одна из граней совпадает со свободной от напряжений поверхностью.

Пусть на двух оставшихся взаимно перпендикулярных площадках будут известны нормальные и касательные напряжения: σ_x, σ_y, τ_yx, τ_xy (рис. 4.3а).

Определим нормальные и касательные напряжения на произвольных площадках, повернутых к заданным на угол α и перпендикулярных к грани, свободной от напряжений.

Ранее было принято следующее правило знаков для нормальных напряжений: растягивающие будем считать положительными, а сжимающие – отрицательными.

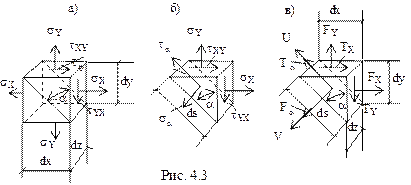
Касательные напряжения будем считать положительными, если они стремятся сдвинуть выделенный элемент по ходу часовой стрелки, и отрицательными – если против хода часовой стрелки.

Проведем наклонное сечение под углом α к вертикальной грани против хода часовой стрелки, отбросим одну часть, приложим к наклонному сечению напряжения 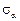и и 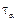рассмотрим равновесие оставшейся части с размерами сторон dx, dy, ds (рис. 4.3б).

В связи с тем, что все размеры выделенной призмы бесконечно малы, касательные и нормальные напряжения по ее боковым и наклонным граням можно считать распределенными равномерно. Поэтому силы, действующие по граням призмы равны произведению площади грани на соответствующее напряжение. Приложим эти силы в центре тяжести соответствующих граней (рис. 4.3в).

Составим следующие уравнения равновесия для выделенной призмы:

1.

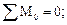
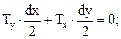
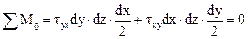, отсюда:

(4.1)

Следовательно, касательные напряжения по двум взаимно перпендикулярным площадкам, действующие по нормали к ребру, равны по абсолютной величине и направлены в противоположные стороны. Эта зависимость между τ_yx и τ_xy называется законом парности касательных напряжений.

2.

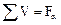
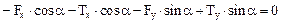
(рис. 4.3в);

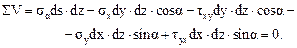
Решим это уравнение относительно σ_α. Учитывая, что 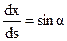, , 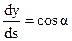после элементарных преобразований, с учетом (4.1) получим:

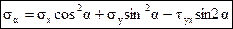. (4.2)

3.

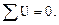
Расписав это уравнение равновесия и используя преобразования, приведенные для второго уравнения равновесия, получим:

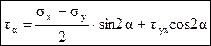. (4.3)

Формулы (4.2) и (4.3) позволяют определять нормальные и касательные напряжения по любым площадкам, проходящим через заданную точку, если известны нормальные и касательные напряжения на двух взаимно перпендикулярных площадках.

Если необходимо определить нормальное напряжение на площадке, перпендикулярной наклонной, то в формулу (4.2) вместо α подставим α+90˚. После указанной подстановки получим

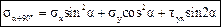. (4.4)

Найдем сумму нормальных напряжений на двух взаимно перпендикулярных площадках σ_α и σ_α+90°, т.е. сложим напряжения по формулам (4.2) и (4.4) и получим:

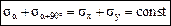, (4.5)

Таким образом, сумма нормальных напряжений на двух взаимно перпендикулярных площадках есть величина постоянная и от положения этих площадок не зависит. Следовательно, если по одной из таких площадок нормальные напряжения имеют максимальное значение, то по другой они имеют минимальное значение.

При расчете инженерных конструкций нет необходимости определять нормальные напряжения по всем площадкам, проходящим через заданную точку. Достаточно знать максимальные и минимальные их значения, которые, как отмечалось ранее, называются главными напряжениями.

Для определения величин главных напряжений и положения главных площадок функцию для σ_α (4.2) исследуем на экстремум, т.е. приравняем нулю первую производную от напряжения σ_α по α при некотором значении угла α = α₀:

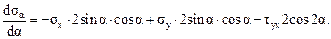
При 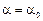, используя известные тригонометрические зависимости, получим:

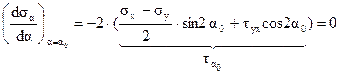. (4.5)′

Здесь α₀ – угол наклона главной площадки к площадке, в которой действуют заданные напряжения σ_х (рис. 4.3б).

Сравнивая выражение (4.5)′ с формулой (4.3), устанавливаем, что .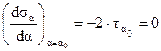

Отсюда следует, что на главных площадках касательные напряжения равны нулю, т.е.:

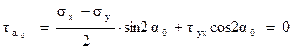. (4.6)

Из соотношения (4.6) получим:

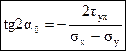, (4.7)

или, используя (4.1):

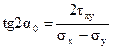. (4.8)

Формулы (4.7) и (4.8) дают значения углов α₀, определяющие две взаимно перпендикулярные площадки, на которых действуют главные напряжения.

Следовательно, для определения положения главных площадок, необходимо площадки, на которых действуют заданные напряжения σ_x и σ_y, повернуть на угол α₀ против хода часовой стрелки (при α₀ > 0) или по ходу часовой стрелки (при α₀ < 0).

Следует иметь в виду, что наибольшее главное напряжение должно проходить в тех четвертях, где сходятся касательные напряжения 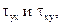и оно всегда находится ближе к тому из заданных нормальных напряжений, значения которого с алгебраической точки зрения больше.

Главные напряжения можно определить, подставляя значения угла α₀ в формулу (4.2).

Эти же напряжения можно определять и без предварительного определения угла α₀, если (4.7) или (4.8) подставить в формулу (4.2). В результате элементарных преобразований получаем следующую формулу для определения величин главных напряжений:

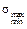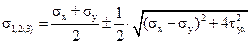= . (4.9)

Определим также площадки, по которым касательные напряжения имеют экстремальные (максимальные и минимальные) значения. Такие площадки, как упоминалось в п. 3.4, называются площадками сдвига.

Для этого приравняем нулю первую производную функции (4.3) при некотором значении угла α₁:

.

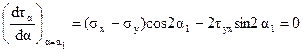Отсюда: 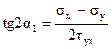. (4.10)

Здесь α₁ – угол наклона площадки сдвига к заданной площадке, по которой действует напряжение σ_х. Если угол α₁ положителен, то эту площадку надо повернуть против хода часовой стрелки, а если отрицателен – то по ходу часовой стрелки.

Формула (4.10) дает значение угла α₁, определяющее положение одной из двух взаимно перпендикулярных площадок. Положение другой площадки определяется поворотом на угол α+90⁰. По одной из двух площадок действует максимальное касательное напряжение τ_max, а по другой – минимальное τ_min. Из закона парности касательных напряжений следует, что

.

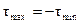Если определены главные площадки, легко определить величины напряжений 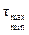и положение площадок, на которых они действуют.

Если в формуле (4.3) для определения касательных напряжений τ_α на произвольной площадке за исходные примем главные напряжения 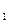σ и σ вместо σ_x и σ_y, а τ_уx = 0, то получим:

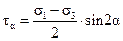. (4.11)

Отсюда следует, что 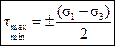, (4.12)

так как sin(2 ) = ±1 при 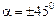, т.е. площадки сдвига наклонены к главным площадкам под углом ±45˚.

Если в формулу (4.12) подставим выражения 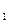σ и σ 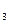из соотношения (4.9), найдем:

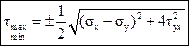. (4.13)

Определим нормальные напряжения на площадках сдвига. Для их определения формулу (4.2) перепишем, подставляя вместо напряжений на произвольных площадках s_х и s_у главные напряжения s₁ и s₃, а t_ух = 0:

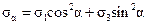. (4.14)

При α = ±45˚ получим формулу для определения нормальных напряжений на площадках сдвига:

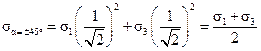. (4.15)

Таким образом, из (4.14) следует, что нормальные напряжения на двух взаимно перпендикулярных площадках сдвига равны между собой по величине и знаку.

Если нормальные напряжения на площадках сдвига равны нулю, то такие площадки называются площадками чистого сдвига.

Примерами чистого сдвига являются кручение и срез.