Расчет с учетом собственного веса
5. Построение эпюры N с учетом собственного веса.
Cобственный вес стержней постоянного сечения учитывается как равномерно распределенная по длине каждого грузового участка нагрузка, направленная вниз. Интенсивность этой распределенной нагрузки равна весу части стержня единичной длины на данном участке.
Для 1-го участка она равна:
q 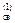 = А
= А  1
1  r = 22,2
r = 22,2  10–3 м2
10–3 м2 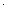 1
1  25 кН/м3
25 кН/м3 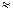 0,56 кН/м.
0,56 кН/м.
Для 2 и 3-го участков, где площадь поперечного сечения равна 2А:
q 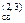 = 2А
= 2А  1
1  r = 44,4
r = 44,4  10–3 м2
10–3 м2  1
1  25 кН/м3
25 кН/м3 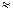 1,12 кН/м.
1,12 кН/м.
N1(х1) = 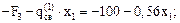
х1 = 0, N1(0) = –100 кН;
х1 = 1,0 м, N1(1,0) = –100,56 кН;
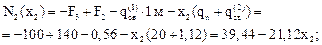
х2 = 0, N2(0) = 39,44 кН;
х2 = 1,2 м, N2(1,2) = 14,11 кН.
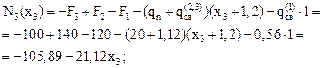 х3 = 0, N3(0) = –105,89 кН;
х3 = 0, N3(0) = –105,89 кН;
х3 = 2,0 м, N3(2,0) = –148,11 кН.
По вычисленным значениям строим эпюру продольных сил N с учетом собственного веса (рис. 3.7в).
6. Определяем нормальные напряжения в сечениях по формуле:
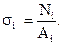
Для этого в пределах каждого грузового участка проведем сечения, бесконечно близкие к началу и к концу участка.
Выпишем площади в указанных сечениях:
На 1-м участке – 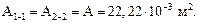
На 2 и 3-м участках:
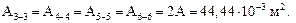
Напряжения в указанных сечениях будут равны:
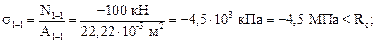
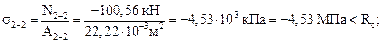
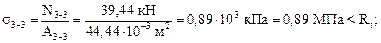
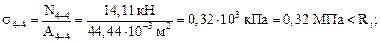
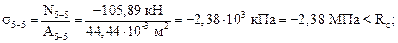
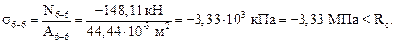
Сравнение с расчетными сопротивлениями на растяжение и на сжатие в соответствующих сечениях показывает, что условия прочности выполняются во всех сечениях, а в сечении 3–3 выполняется практически со знаком равенства. Это говорит о том, что площади сечений подобраны верно.
Ввиду того, что площадь поперечного сечения рассчитывается по эпюре продольных сил, построенной без учета собственного веса, а напряжения определяются по эпюре N, построенной с учетом собственного веса, возможны перенапряжения в некоторых сечениях. В таких случаях, если перенапряжение больше 5 %, необходимо несколько увеличить площадь поперечного сечения.
По вычисленным значениям строим эпюру нормальных напряжений с учетом собственного веса бруса (рис. 3.8б).
7. Определение абсолютных деформации участков бруса.
В общем случае абсолютные деформации грузовых участков определяются по формуле (3.14):
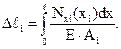
При Е×Аi = const интеграл 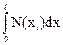 равен площади эпюры продольных сил на i-м грузовом участке.
равен площади эпюры продольных сил на i-м грузовом участке.
Так как при учете собственного веса на любом грузовом участке эпюра продольных сил имеет вид трапеции, то абсолютную деформацию этого участка можно вычислить по формуле:
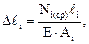
где Ni(ср) – средняя линия трапеции.

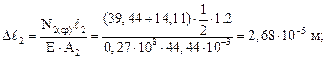
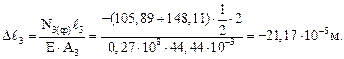
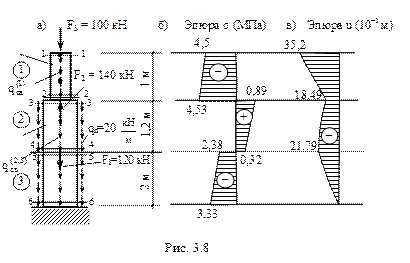
По формуле (3.16), используя найденные значения 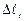 , определяем перемещение сечений ui–i
, определяем перемещение сечений ui–i  (при этом будем иметь в виду, что сечение 5–5 бесконечно близко к сечению 4–4, а сечение 3–3 бесконечно близко к сечению 2–2):
(при этом будем иметь в виду, что сечение 5–5 бесконечно близко к сечению 4–4, а сечение 3–3 бесконечно близко к сечению 2–2):
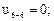
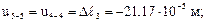
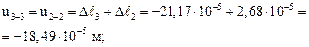
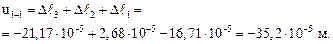
Далее строим эпюру перемещений сечений u, откладывая перемещения в каждом сечении перпендикулярно оси бруса (рис. 3.8в).
Так как в подынтегральном выражении формулы (3.14) функция N(x) на всех участках нашего бруса есть полином первой степени, эпюра перемещений на этих участках изменяется по закону квадратной параболы.
В местах приложения внешних сосредоточенных сил параллельных оси бруса на эпюре перемещений u имеет место излом линии эпюры.
8. Проверка жесткости бруса.
Из эпюры перемещений u видно, что 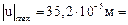 =
= 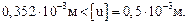 Условие жесткости выполняется.
Условие жесткости выполняется.
Дата добавления: 2021-12-14; просмотров: 503;











