Нормально распределённой совокупности.

Пусть из генеральной совокупности, значения которой распределены по нормальному закону с неизвестной дисперсией 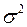, взята случайная выборка из n независимых наблюдений и вычислена выборочная дисперсия S².

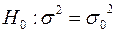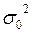Требуется проверить нулевую гипотезу , где - определённое значение генеральной дисперсии. Для проверки нулевой гипотезы используют статистику

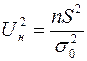, (10)

которая при выполнении гипотезы 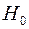имеет распределение 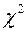с 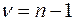степенями свободы.

В зависимости от конкурирующей гипотезы рассматривают левостороннюю, правостороннюю или двустороннюю критические области. Границы критических областей определяют по таблице распределения 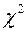- Пирсона.

Рассмотрим три случая:

1. Если 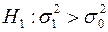, то выбирают правостороннюю критическую область и 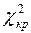находят из условия

.

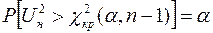Правила проверки гипотезы заключаются в следующем:

1) если 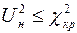, то нулевая гипотеза не отвергается;

2) если 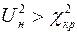, то нулевая гипотеза отвергается.

2. Если 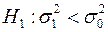, то строят левостороннюю критическую область и 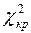находят из условия

.

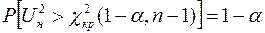Правила проверки гипотезы заключаются в следующем:

1) если 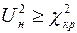, то гипотеза не отвергается;

2) если 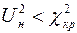, то гипотеза отвергается

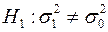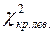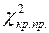3. Если , то строят двустороннюю критическую область и её границы и находят из условий:

;

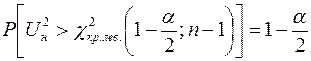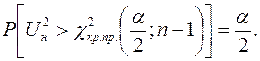
Правила проверки гипотезы заключается в следующем:

Если 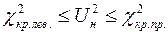, то гипотеза не отвергается, в противном случае отвергается.

Пример 1. Точность работы автоматической линии проверяют по дисперсии контролируемого признака, которая не должна превышать 0,1 мм². По результатам выборочного контроля получены следующие данные:

Требуется проверить на уровне значимости 0,01, обеспечивает ли линия требуемую точность.

Решение: Задача состоит в проверке гипотезы о значении генеральной дисперсии 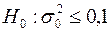. Автоматическая линия не обеспечивает требуемую точность, если 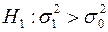, следовательно, в данном случае строим правостороннюю критическую область.

Для вычисления статистики 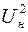по формуле (10), необходимо найти выборочную дисперсию 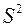. Примем значение C = 43,8, а вычисление оформим в таблице:

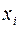
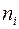
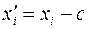
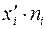
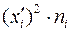
43,0		- 0,8	- 2,4	1,92
43,5		- 0,3	- 2,1	0,63
43,8
44,4		0,6	4,8	2,88
44,6		0,8	1,6	1,28
Итого:		-	1,9	6,71

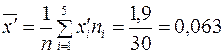
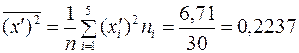
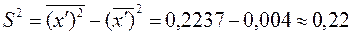
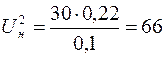
По таблице 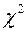- распределения при заданном уровне значимост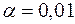и и 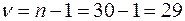получаем .

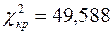Сравнивая 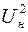и 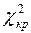, делаем вывод о том, что гипотеза 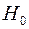отвергается. Это значит, что генеральная дисперсия не равна 0,1, линия не обеспечивает заданную точность и требуется её регулировка.