Нормально распределённой совокупности

Пусть из генеральной совокупности X, значения признака имеют нормальный закон распределения с параметрами 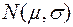при неизвестном математическом ожидании, взята случайная выборка объёма n и вычислена средняя арифметическая 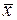, а

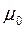и 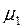- определённые значения параметра 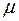. Для проверки нулевой гипотезы 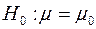при конкурирующей гипотезе 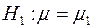, в случае, когда значение 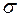генеральной совокупности известно, используется статистика

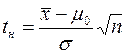, (5)

которая при выполнении нулевой гипотезы имеет нормированное нормальное распределение .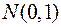

Согласно требованию к критической области при 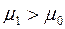выбирают правостороннюю критическую область, при 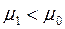- левостороннюю, при 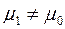- двустороннюю критическую область.

Границы критической области 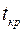определяют по интегральной функции Лапласа 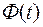из условий:

в случае односторонней критической области:

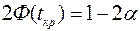, (6)

в случае двусторонней критической области:

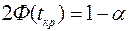. (7)

При проверке гипотезы 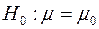при неизвестнойгенеральной дисперсии 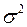используется статистика

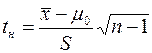, (9)

которая при выполнении нулевой гипотезы имеет распределение Стьюдента с числом степеней свободы равном .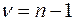

Границы критической области 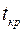определяют по таблице t-распределения для заданного уровня значимости 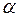при двусторонней критической области или 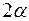, если область односторонняя, и числом степеней свободы .

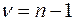Правила проверки гипотезы сводятся к следующему:

1) при левосторонней критической области, если 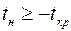, нулевая гипотеза не отвергается;

2) при правосторонней критической области, если 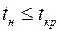, то

нулевая гипотеза не отвергается;

3) при двусторонней критической области, если 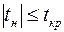, то нулевая гипотеза не отвергается.

При выполнении противоположных неравенств нулевая гипотеза 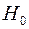отвергается.