Выборка из генеральной совокупности. Вариационный ряд. Гистограмма относительных частот

В математической статистике применяются следующие термины. Множество всех возможных значений случайной величины 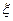называется генеральной совокупностью.

Пусть с испытанием связана случайная величина 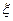и пусть в результате серии n независимых испытаний получен набор значений :

.

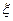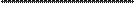
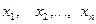Данный набор чисел называется выборкойиз генеральной совокупности, число n называется объемом выборки, числа называются элементами выборки. Элементы выборки, расположенные в порядке возрастания называются вариационным рядом:

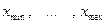- вариационный ряд.

Число 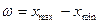называется размахом выборки.

Выполним следующие построения:

. . .

. . .

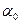
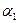
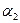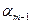
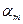
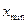
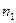
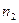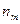
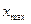
рис. 1

1) разделим отрезок 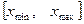на некоторое число m интервалов одинаковой длины .

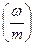2) подсчитаем число элементов выборки, попадающих в каждый интервал:

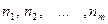- частоты попадания в интервал.

Очевидно, .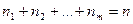

3) составим таблицу

Таблица 1.

.

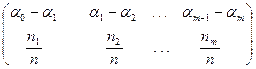Элементы второй строки называются относительными частотами попадания в интервал. Эта таблица называется выборочным распределением случайной величины .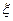

Очевидно, .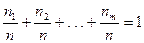

4) изобразим выборочное распределение на графике

f^* (x)

. . .

х

. . .

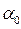
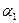
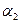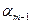
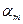
рис. 2

За единицу масштаба на оси абсцисс примем длину интервала 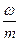. Очевидно, площадь построенной ступенчатой фигуры равна единице.

Построенный график называется гистограммой относительных частот и представляет собой выборочный аналог плотности вероятности случайной величины.