Лекция 5. Элементы корреляционного анализа
Задачи корреляционного анализа.
Двумерная корреляционная модель
Главной задачей корреляционного анализа является оценка взаимосвязи между переменными величинами на основе выборочных данных.
Различают два вида зависимостей: функциональную и стохастическую. При функциональной зависимости каждому значению одной случайной величины ставится в соответствие определённое значение другой величины.
При изучении массовых явлений зависимость между наблюдаемыми величинами проявляется лишь тогда, когда число элементов изучаемой совокупности велико. При этом каждому значению одной величины соответствует целое распределение другой. В этом случае говорят о стохастической или корреляционной зависимости.
При изучении корреляционной зависимости между переменными возникают следующие задачи:
- Измерение силы (тесноты) связи;
- Обнаружение неизвестных причин связей;
- Построение корреляционной модели и оценка её параметров;
- Проверка значимости параметров связи;
- Интервальное оценивание параметров связи.
Рассмотрим случай изучения корреляционной зависимости между двумя признаками Y и X. Построение двумерной корреляционной модели предполагает, что закон распределения двумерной случайной величины в генеральной совокупности является нормальным. Это условие обеспечивает линейный характер связи между изучаемыми признаками, что даёт право на использование в качестве показателя тесноты связи парного коэффициента корреляции.
Выделим две основные задачи:
1) Определение формы связи, т.е. нахождение по заданной корреляционной таблице уравнений связи между значениями переменной X и групповыми средними значений переменной Y и наоборот:
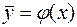 или
или 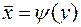 .
.
Эти уравнения называют уравнениями регрессии Y на X и X на Y соответственно. Если зависимость линейная, то будем говорить о прямых регрессии.
2) Установление тесноты связи, т.е. оценка степени рассеяния значений переменной Y около прямой регрессии для различных значений переменной X.
Рассмотрим решение этих задач на конкретном примере , взятом из книги [3].
Задача: В результате обработки опытных данных получено распределение 100 га пахотной земли по количеству внесенных удобрений X (ц на 1 га) и по урожайности Y (ц с 1 га), представленное в таблице:
Таблица 1.
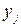
| Итого
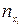
| ||||||
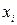
| |||||||
| - | - | - | |||||
| - | - | ||||||
| - | - | ||||||
| - | - | ||||||
Итого 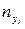
|
При каждом фиксированном значении 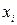 рассмотрим распределение величины
рассмотрим распределение величины 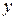 и вычислим средние арифметические
и вычислим средние арифметические 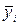
Для 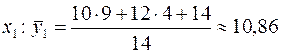
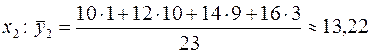
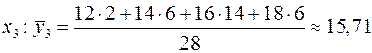
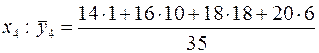
Запишем полученную зависимость в таблицу:
Таблица 2.
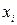
| ||||
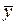
| 10,86 | 13,22 | 15,71 | 17,66 |
Совершенно аналогично, рассматривая теперь распределения по столбцам таблицы 1, для каждого 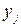 найдём средние групповые
найдём средние групповые 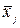 :
:
Для 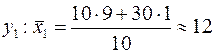
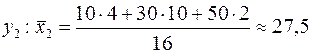
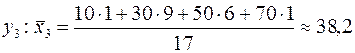
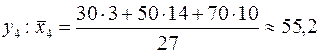
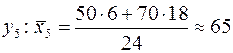
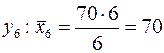
Таблица 3.
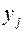
| ||||||
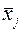
| 27,5 | 38,2 | 55,2 |
Отметим на плоскости XOY точки из таблиц 2 и 3. Соединим их ломанной, получим эмпирические линии регрессии:
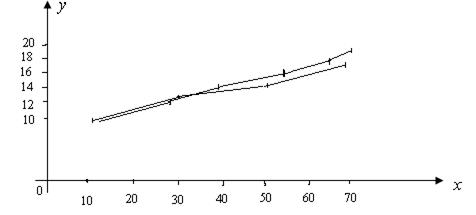
Построенные линии позволяют сделать вывод о существовании линейной корреляционной зависимости между Х и Y. Эту зависимость построим в виде уравнения прямой регрессии
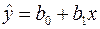 (1)
(1)
Уравнение (1) служит оценкой уравнения линейной регрессии в генеральной совокупности
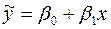 (2)
(2)
Для отыскания оценочных значений коэффициентов уравнения b0 и b1 применим метод наименьших квадратов (МНК).
Пусть 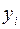 фактическое значение зависимой переменной, а
фактическое значение зависимой переменной, а 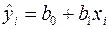 - расчетное значение. Ставится задача: подобрать коэффициенты
- расчетное значение. Ставится задача: подобрать коэффициенты 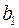 и
и  так, чтобы сумма квадратов отклонений фактических значений зависимой переменной от расчетных была минимальна, т.е.
так, чтобы сумма квадратов отклонений фактических значений зависимой переменной от расчетных была минимальна, т.е.
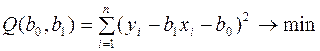 (3)
(3)
Для того чтобы найти минимум функции (3), находят частные производные первого порядка, затем приравнивают их к нулю и решают полученную систему уравнений:
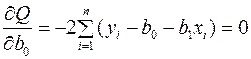
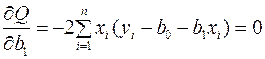
Раскрыв скобки, получим, так называемую систему нормальных уравнений:
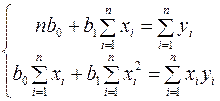 (4)
(4)
Введем следующие обозначения:
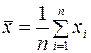 ;
; 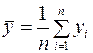 ;
; 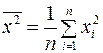 ;
; 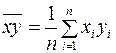 ;
; 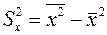
Тогда из системы (4), с учетом введенных обозначений, найдем:
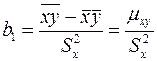 (5)
(5)
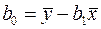
Коэффициент  является средним значением
является средним значением 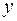 в точке
в точке 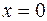
и поэтому не имеет какой-либо экономической интерпретации. На практике больший интерес представляет коэффициент регрессии 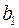
Парный коэффициент корреляции, характеризующий тесноту линейной связи между X и Y, определяется как математическое ожидание произведения их нормированных величин:
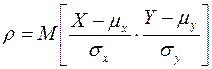
Выборочная оценка коэффициента корреляции равна
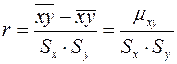 (6)
(6)
Здесь 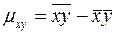 - выборочный корреляционный момент. Коэффициент
- выборочный корреляционный момент. Коэффициент 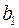 часто называют коэффициентом прямой регрессии
часто называют коэффициентом прямой регрессии 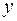 на
на 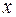 и обозначают
и обозначают 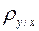 . С учетом формулы (5), коэффициент корреляции можно вычислять по формуле
. С учетом формулы (5), коэффициент корреляции можно вычислять по формуле
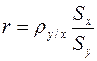 (7)
(7)
Уравнение прямой регрессии 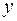 на
на 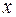 записывается в виде:
записывается в виде:
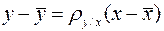 (8)
(8)
В двумерной модели проводится проверка значимости (существенности) параметров 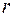 и
и 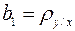 . Проверяется гипотеза об отсутствии линейной корреляции в генеральной совокупности, т.е.
. Проверяется гипотеза об отсутствии линейной корреляции в генеральной совокупности, т.е. 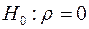 . Известно, что если верна нулевая гипотеза
. Известно, что если верна нулевая гипотеза 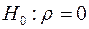 , то статистика
, то статистика
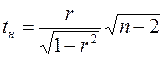 (9)
(9)
имеет распределение Стьюдента с числом степеней свободы 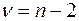 . По таблице распределения Стьюдента находят критическое значение
. По таблице распределения Стьюдента находят критическое значение 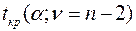 и сравнивают его с
и сравнивают его с 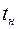 . Если
. Если 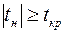 , то гипотеза отвергается. А это значит, что гипотеза о наличии линейной зависимости не противоречит опыту и её можно принять на данном уровне значимости
, то гипотеза отвергается. А это значит, что гипотеза о наличии линейной зависимости не противоречит опыту и её можно принять на данном уровне значимости 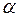 . В таком случае говорят, что коэффициент корреляции
. В таком случае говорят, что коэффициент корреляции 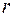 значим или достоверен на уровнен значимости
значим или достоверен на уровнен значимости 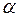 .
.
Последуем рассмотренной теории в решении начатой выше задачи. Найдем 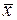 и
и 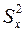 по формулам (1) и (2) лекции 1, при
по формулам (1) и (2) лекции 1, при 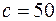 и
и 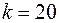
Таблица 4.
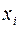
| 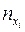
| 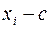
| 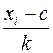
| 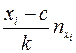
| 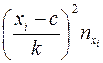
|
| -40 | -2 | -28 | |||
| -20 | -1 | -23 | |||
| Итого: | - | - | -16 |
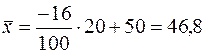 ;
;
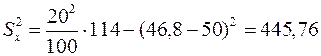 ;
; 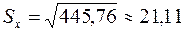
Аналогично рассчитываем 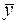 и
и 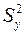 , при
, при 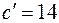 и
и 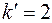
Таблица 5.
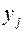
| 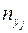
| 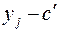
| 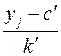
| 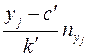
| 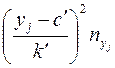
|
| -4 | -2 | -20 | |||
| -2 | -1 | -16 | |||
| Итого: | - | - |
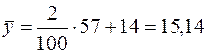 ;
;
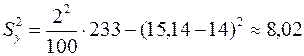 ;
; 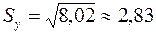
Для подсчета коэффициента регрессии 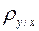 необходимо вычислить
необходимо вычислить 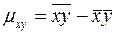 . Непосредственное вычисление этой разности приводит к громоздким расчетам. Эти расчеты упрощаются, если использовать формулу:
. Непосредственное вычисление этой разности приводит к громоздким расчетам. Эти расчеты упрощаются, если использовать формулу:
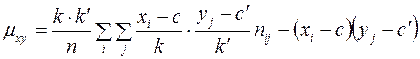 (10)
(10)
С целью упорядочения промежуточных вычислений поместим их в таблицу:
Таблица 6.

| 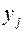
| Итого: | |||||||
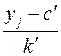
| -2 | -1 | |||||||
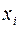
| 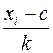
| ||||||||
| (1) | (2) | (3) | (4) | (5) | (6) | (7) | (8) | (9) | (10) |
| -2 | 94 | 42 | 10 | - | - | - | - | ||
| -1 | 12 | 101 | 90 | 3-1 | - | - | -3 | ||
| - | 20 | 60 | 140 | 60 | - | - | - | ||
| - | - | 10 | 101 | 182 | 63 | - | |||
| Итого: | - | -3 | - | - | -3 | ||||
| - | - | - | - |
В таблице на пересечении строк и столбцов записаны частоты 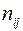 , взятые из таблицы 1 и снабженные индексом равным произведению измененных значений
, взятые из таблицы 1 и снабженные индексом равным произведению измененных значений 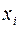 и
и 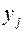 , например: на пересечении первой строки и первого столбца стоит число 94. Здесь 9 – частота первоначальных значений x и y, индекс 4 = (-2)(-2). Вся таблица разбита нулевой строкой и нулевым столбцом на четыре части. В столбце (9) подсчитывается сумма произведений частот на индексы построчно в I и III частях:
, например: на пересечении первой строки и первого столбца стоит число 94. Здесь 9 – частота первоначальных значений x и y, индекс 4 = (-2)(-2). Вся таблица разбита нулевой строкой и нулевым столбцом на четыре части. В столбце (9) подсчитывается сумма произведений частот на индексы построчно в I и III частях: 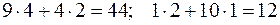 . В столбце (10) – соответствующие суммы во II и IV частях. Нумерация частей идет по контуру буквы Z. Сумма чисел последних четырех клеток:
. В столбце (10) – соответствующие суммы во II и IV частях. Нумерация частей идет по контуру буквы Z. Сумма чисел последних четырех клеток: 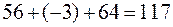 - соответствует двойной сумме в формуле (10). Нижние строки «Итого» служат для контроля правильности вычислений. Таким образом:
- соответствует двойной сумме в формуле (10). Нижние строки «Итого» служат для контроля правильности вычислений. Таким образом:
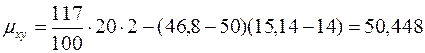
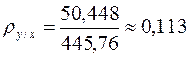
Подставляя найденные значения в формулу (8), получим уравнение прямой регрессии y на x:
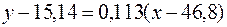 или
или 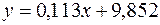
Вычислим коэффициент прямой регрессии x на y по формуле
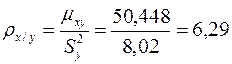
Соответствующее уравнение прямой имеет вид:
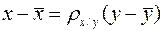
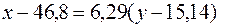 или
или 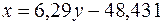
Выборочный коэффициент корреляции равен:
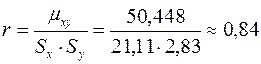
С целью оценки достоверности коэффициента корреляции воспользуемся критерием Стьюдента, описанным выше. Найдем значение наблюдаемой статистики по формуле (9):
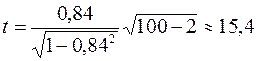
В таблице критических точек распределения Стьюдента значение 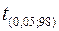 , соответствующее уровню значимости
, соответствующее уровню значимости 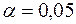 и числу степеней свободы
и числу степеней свободы 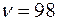 , отсутствует. Однако оно находится между
, отсутствует. Однако оно находится между 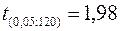 и
и 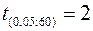 , и явно меньше наблюдаемого значения. Следовательно, выборочный коэффициент корреляции достоверен на уровне значимости 0,05 и в генеральной совокупности можно принять линейную зависимость.
, и явно меньше наблюдаемого значения. Следовательно, выборочный коэффициент корреляции достоверен на уровне значимости 0,05 и в генеральной совокупности можно принять линейную зависимость.
Дата добавления: 2021-12-14; просмотров: 454;











