Понятие о критериях согласия

Найденные в примере теоретические частоты несколько отличаются от эмпирических частот. Такое несовпадение возможно по двум причинам:

1. Они не существенны и являются следствием случайности единичных наблюдений. И предположение о распределении изучаемого признака в соответствии с выбранным теоретическим законом согласуется с данными выборки.

2. Они не случайны, опытное и теоретическое распределения не согласуются, они противоречат друг другу. Следовательно, гипотезу о распределении по выбранному закону следует признать ошибочной.

Возможность сделать первый или второй вывод позволяют сделать, так называемые критерии согласия.

Критерий состоит в том, что выбранная некоторая случайная величина Y является мерой расхождения (рассогласования) между вариационным рядом и предполагаемым законом распределения. При проверке нулевой гипотезы о виде теоретического закона распределения, заранее задаётся уровень значимости 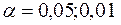и т.д. Затем на основании закона распределения находят такое значение Y_кр, что

.

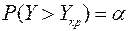Критическое значение Y_кр обычно находят по таблице соответствующей функции распределения. Далее вычисляется на основании выборки наблюдаемое значение статистики критерия Y_н. Наконец, сравниваются значения Y_н и Y_кр. Если Y_н>Y_кр, то нулевая гипотеза отвергается. В противном случае гипотеза не отвергается, т.е. отклонения от предполагаемого закона считаются незначительными.

Можно осуществить проверку гипотезы и в другом порядке: по наблюдаемому значению статистики Y_н определяется из таблицы 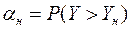. Если 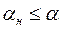, то гипотеза отвергается. Если 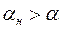, то гипотеза не отвергается.

Критерий согласия 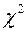Пирсона

В качестве меры расхождения берётся величина

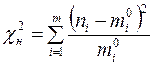, (4)

где 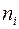- эмпирические частоты случайной величины Х;

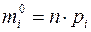- теоретические частоты, рассчитанные по предполагаемому закону распределения случайной величины Х.

Наблюдаемая статистика 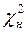имеет распределение Пирсона с числом степеней свободы .

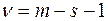m – число интервалов эмпирического распределения;

s – число параметров теоретического распределения.

В случае нормального распределения s = 2, .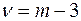

Схема применения критерия 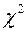- Пирсона сводится к следующему:

1. Вычисляется статистика 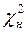по формуле (4);

2. Для выбранного уровня значимости 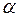по таблице 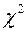- распределения находят критическое значение ;

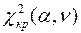3. Правило проверки состоит в следующем: если 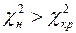, то гипотеза 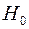отвергается, если 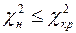, то не отвергается, т.е не противоречит опытным данным.

Пример 2. Используя данные примера 1 на уровне значимости 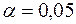проверить гипотезу о нормальном распределении случайной величины Х – выработки рабочих, с помощью критерия 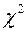- Пирсона.

Решение: Составим таблицу расчета наблюдаемого значения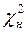

Эмпирические частоты	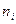Теоретические частоты	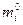Разность
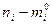
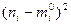
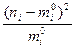
	4,89	1,11	1,23	0,25
	23,86	-3,86	14,9	0,624
	40,38	4,62	21,34	0,528
	24,79	-0,79	0,62	0,025
	5,3	-0,3	0,09	0,017
	99,22	-	-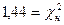

Так как число интервалов 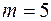, число параметров S = 2, то число степеней свободы 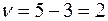. По таблице 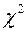- распределения находим значение 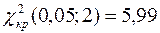. Видим, что 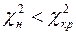. Следовательно, гипотеза о нормальном распределении генеральной совокупности может быть принята, и она согласуется с опытными данными.