Понятие статистической гипотезы и статистического критерия.

Статистической гипотезой называют любое предложение о виде неизвестного закона распределения случайной величины или значении его параметров.

Пусть 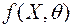- закон распределения случайной величины Х, зависящей от одного параметра 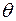. Предположим, что надо проверить гипотезу о том, что 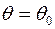. Назовём эту гипотезу нулевой (проверяемой) и обозначим её через 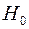. Противоположную гипотезу, например, 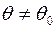, назовём конкурирующей и обозначим через .

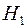Задача заключается в проверке гипотезы 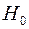относительно конкурирующей гипотезы 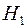на основании выборки, состоящей из n независимых наблюдений .

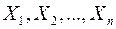Принцип проверки заключаются в следующем: всё множество выборок объёмом n можно разбить на два непересекающихся подмножества (обозначим их через Q и W) таких, что проверяемая гипотеза должна быть отвергнута, если наблюдаемая выборка попадает в подмножество W, и принята, если наблюдаемая выборка принадлежит подмножеству Q. Подмножество W называют критической областью, Q – областью допустимых значений.

Вывод о принадлежности данной выборки тому или иному подмножеству делают на основании статистического критерия.

Основой критерия является специально составленная выборочная характеристика (статистика) 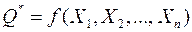, точное или приближённое распределение которой известно.

Если наблюдаемое значение статистики критерия попадает в критическую область, то гипотезу отвергают, если же оно попадает в область допустимых значений, то гипотезу не отвергают.

При использовании этого принципа возможны ошибки двух видов:

- гипотеза H₀ верна, но её отвергают согласно критерию, т.е.

допускается ошибка, которую принять называть ошибкой первого рода;

-гипотеза H₀ неверна, и её принимают согласно критерию, т.е.

допускается ошибка второго рода.

Уровнем значимости 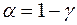называют вероятность совершить ошибку первого рода. С уменьшением 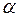возрастает вероятность ошибки второго рода.

Мощностью критерия 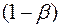называют вероятность того, что нулевая гипотеза H₀ будет отвергнута, если верна конкурирующая гипотеза, т.е. вероятность не допустить ошибку второго рода.

Обозначим через 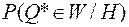вероятность попадания статистики критерия 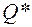в критическую область W, если верна соответствующая гипотеза H.

Тогда требования к критической области можно выразить следующим образом:

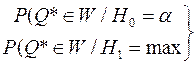(1)

Таким образом, критическую область надо выбирать так, чтобы вероятность попадания в неё статистики была минимальна, если гипотеза H₀ верна, и максимальна в противном случае.

В зависимости от конкурирующей гипотезы H₁ выбирают правостороннюю, левостороннюю или двустороннюю критические области.

Границы областей находят из следующих условий:

при правосторонней критической области

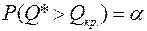(2)

при левосторонней критической области

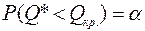(3)

при двусторонней критической области

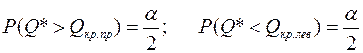(4)