Вычисление теоретического ряда частот

Пусть дискретная случайная величина Х, принимающая значения 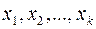, с вероятностями 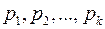, характеризует некоторый признак в генеральной совокупности достаточно большого объёма. Тогда события 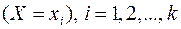составляют полную группу. Образуя из этой генеральной совокупности собственно-случайную выборку, мы придем к схеме независимых испытаний. Поэтому вероятность того, что при отборе каждого элемента выборки рассматриваемый признак примет значение 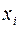, можно считать постоянной равной .

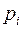Теоретической частотой 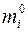события 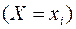в n независимых испытаниях назовём математическое ожидание числа наступлений этого события. Тогда

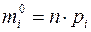(1)

Если случайная величина Х непрерывна и множеством её значений является прямая или её часть, то разбивая это множество на непересекающиеся интервалы 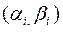, получим

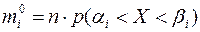(2)

Наиболее часто встречающийся закон распределения непрерывной случайной величины – это нормальный закон. Для нормального закона распределения формула (2) примет вид:

(3)

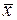где и 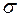- выборочные оценки математического ожидания и дисперсии генеральной случайной величины.

Пример 1. Получено следующее распределение 100 рабочих цеха по выработке в отчётном году (в процентах к прошлому году):

Предполагая, что распределение случайной величины Х – выработки рабочих – является нормальным, вычислить теоретический ряд частот. Построить гистограмму и соответствующую нормальную кривую теоретического распределения.

Решение:Параметры теоретического распределения неизвестны. Заменим их выборочными оценкам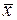и и 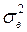, которые вычислим так же, как это сделано в примере 1 лекции 1: ,

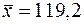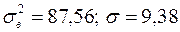. Для расчёта теоретических частот с помощью формулы (3), составим таблицу

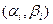
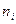
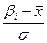
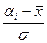
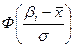
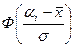
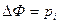
Интервалы	Эмпири- ческие частоты					Вероят- ности	Теорети- ческие частоты
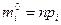
94-104		-1,62	-2,69	-0,4474	-0,4963	0,0489	4,89
104-114		-0,55	-1,62	-0,2088	-0,4474	0,2386	23,86
114-124		0,51	-0,55	0,1950	-0,2088	0,4038	40,38
124-134		1,58	0,51	0,4429	0,1950	0,2479	24,79
134-144		2,64	1,58	0,4959	0,4429	0,053	5,3
Итого:		-	-	-	-	0,9922	99,22

Построим гистограмму по данному интервальному вариационному ряду и в той же системе координат теоретическую кривую, принимая за варианты середины интервалов.

Х

94 104 114 124 134 144