Перестановки с повторением

Пусть дано множество X = {x₁, x₂, …, x_r}. Составим кортеж длиной n, в который элемент x₁ входит n₁ раз, x₂ – n₂ раза,…, x_r - n_r раз. Назовем составом этого кортежа новый кортеж (n₁, n₂, …, n_r). Кортежи данного состава называют перестановками с повторением из n₁ элементов х₁, n₂ элементов х₂,…, n_r элементов x_r. Их число выражается формулой

,

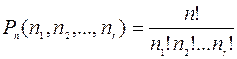где .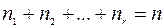

Лекция 2. Пространство элементарных событий.
Классическое определение вероятности

Реализация некоторой совокупности условий называется испытанием, а результат испытания – событием. События будем обозначать большими латинскими буквами A, B, C, D,… Все события делят на три вида: достоверные, невозможные и случайные.

Достоверным называется событие, которое обязательно произойдет при выполнении данного комплекса условий.

Пример 1. При бросании игральной кости выпало число очков не более 6 – есть достоверное событие.

Невозможным называется событие, которое заведомо не произойдет, если будут выполнены данные условия.

Пример 2. При бросании игральной кости выпало число очков равное 8 – есть событие невозможное.

Случайным называется событие, которое может произойти или не произойти при выполнении данного комплекса условий.

Пример 3. При бросании игральной кости выпало 5 очков – это случайное событие.

Каждое случайное событие зависит от многих причин, но законы воздействия некоторых из них на конечный результат, как правило, неизвестны. Так, результат бросания монеты зависит от силы бросания, вращающего момента, ровности поверхности и т. д.

Поэтому заранее предугадать исход отдельного испытания невозможно, да этого и не требуется на практике. Например, для анализа деятельности предприятия неважно, является ли конкретная деталь стандартной или нет. Гораздо важнее знать, как часто встречается брак в выпускаемых изделиях. Или, при посеве семян, важно знать какой процент семян взойдет. Результат отдельного испытания для отдельного зернышка никакой практической ценности не имеет.

В рассмотренных примерах, во-первых, мы имеем дело с так называемыми массовыми испытаниями, которые состоят из повторения большого числа подобных между собой единичных испытаний, при соблюдении определенных условий их проведения. Во-вторых, в этих массовых однородных испытаниях мы не пытаемся предсказать исход отдельного испытания.

Массовые однородные случайные события, наступающие в результате описанных испытаний, подчиняются определенным закономерностям, которые называют вероятностными законами.

Предметом теории вероятностей является изучение закономерностей массовых, однородных, случайных событий.