Сочетания без повторений

Сочетанием без повторения из n элементов по m называется любое неупорядоченное подмножество множества N, содержащее m различных элементов.

Из определения следует, что два сочетания различаются только элементами, порядок не важен.

Теорема 5. Число сочетаний без повторений вычисляют по одной из следующих формул:

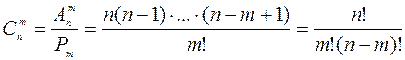
Пример 1. В комнате 5 стульев. Сколькими способами можно разместить на них

а) 7 человек; б) 5 человек; в) 3 человека?

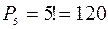Решение: а) Прежде всего надо выбрать 5 человек из 7 для посадки на стулья. Это можно сделать способом. С каждым выбором конкретной пятерки можно произвести перестановок местами. Согласно теореме умножения искомое число способов посадки равно .

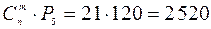Замечание: Задачу можно решать, используя только теорему произведения, рассуждая следующим образом: для посадки на 1-й стул имеется 7 вариантов, на 2-й стул-6 вариантов, на 3-й -5, на 4-й -4 и на 5-й -3. Тогда число способов посадки 7 человек на 5 стульев равно 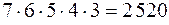. Решения обоими способами согласуются, так как

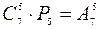
б) Решение очевидно -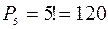

в) 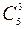- число выборов занимаемых стульев.

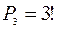- число размещений трех человек на трех выбранных стульях.

Общее число выборов равно .

Не трудно проверить формулы ;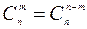

;

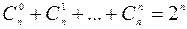- число всех подмножеств множества, состоящего из n элементов.