Приведенный момент инерции и приведенный момент сил

Если в формулу (6.1) или (6.2) подставить значения кинетической энергии механизма и суммы работ всех сил, получим уравнение с несколькими неизвестными v_sk , 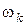, , 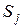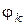. Кинематический анализ механизма позволяет выразить их через характеристики движения начального звена, составляя дополнительные уравнения, связывающие неизвестные координаты и скорости через обобщенную координату и обобщенную скорость. В результате получается громоздкая система уравнений. Чтобы упростить решение задачи, составляют более удобное для исследования уравнение движения воображаемого звена – звена приведения, которое движется так же, как начальное звено механизма. Рассмотрим случай, когда в качестве начального выбрано звено, совершающее вращательное движение. Такое же движение должно совершать звено приведения, заменяющее механизм. Момент инерции 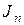звена приведения называется приведенным моментом инерции, а 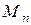момент условной пары сил, вращающей звено приведения, приведенным моментом сил.

Очевидно, что уравнение движения звена приведения и уравнение движения реального механизма (машины) должны быть тождественными, так как координата и скорость звена приведения в любой момент времени равны обобщенной координате 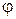и обобщенной скорости 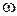. Тогда в соответствии с уравнениями (6.1) и (6.2), кинетические энергии звена приведения и всего механизма, а также элементарная работа приведенного момента сил и сумма элементарных работ фактически действующих сил должны быть равны в любом положении механизма:

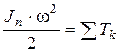, (6.11)

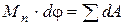. (6.12)

Подставляя в формулу (6.11) значение 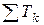по формуле (5.6), после преобразования получаем

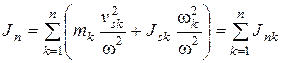. (6.13)

Приведенный момент инерции механизма равен сумме приведенных моментов инерции всех его звеньев. Приведенный момент инерции звена каждого звена механизма определяется из условия равенства кинетической энергии этого звена и кинетической энергии соответствующей массы, присоединяемой к звену приведения.

Чтобы в формуле (6.12) избавиться от бесконечно малых величин, учтем, что отношение выполненной работы ко времени ее выполнения равно мощности:

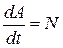. (6.14)

Подставляя сюда значения элементарной работы (6.5) и (6.7), получаем формулы для вычисления мощностей силы и вращающего момента:

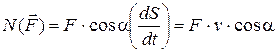, (6.15)

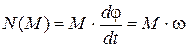. (6.16)

Тогда из равенства (6.12), подставив в него сумму элементарных работ (6.10) и разделив на dt, а затем на 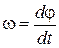, найдем

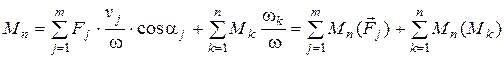. (6.17)

Приведенный момент сил равен сумме приведенных моментов от всех действующих сил. Условием приведения сил является равенство мощности приведенного момента и мощности действующих сил.

Приведенный момент сил М_п для технологической машины, состоящей из жестких звеньев, в общем случае можно представить как алгебраическую сумму нескольких моментов:

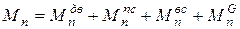, (6.18)

где 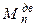– приведенный момент сил, развиваемых двигателем; 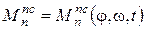– приведенный момент от сил производственного сопротивления; 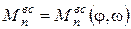– приведенный момент от сил вредного сопротивления – трения в кинематических парах и сопротивления среды; 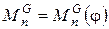– приведенный момент от сил тяжести звеньев.

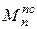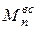Моменты и технологической машины отрицательны, момент 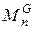может изменять знак в зависимости от движения центров масс звеньев, момент 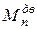положительный. В грузоподъемной машине во время опускания груза его сила тяжести становится движущей силой. Приведенный момент от этой силы будет положительным, а момент двигателя отрицательным. Электродвигатель в этом случае работает в генераторном режиме.

Основное удобство приведенного момента инерции и приведенного момента сил заключается в том, что для их определения достаточно знать отношения скоростей 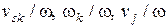, которые не зависят от действительных величин этих скоростей: во сколько раз изменяется 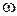, во столько же раз изменяются величины 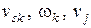. Отношения скоростей можно найти при кинематическом анализе механизма, задавая начальному звену любое удобное для исследования движение. Следовательно, приведенные моменты могут быть вычислены заранее, еще до решения уравнений движения механизма (машины).

Анализ формулы (6.13) показывает, что приведенный момент инерции имеет постоянную величину для зубчатых механизмов, в которых передаточные отношения колес не изменяются в процессе движения. В рычажных и кулачковых механизмах отношения скоростей, а значит, и величина приведенного момента инерции зависят от положения начального звена. Величина приведенного момента сил зависит не только от отношения скоростей, но и от того, каким являются сами действующие силы: 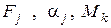в формуле (6.17). Они могут быть постоянными, зависеть от положения и скорости точки приложения или от времени.