Уравнения движения механизма и машины

Определив приведенный момент инерции (6.13) и приведенный момент сил (6.17), можно записать закон изменения кинетической энергии звена приведения:

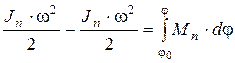. (6.19)

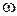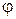Здесь и , по определению звена приведения, в любой момент времени равны угловой скорости и координате начального звена, т.е. обобщенной скорости и обобщенной координате машины (механизма). Следовательно, уравнение (6.19) является уравнением движения машины в форме интеграла кинетической энергии.

Закон движения машины в дифференциальной форме можно получить из уравнения (6.2). Подставим в него кинетическую энергию звена приведения ( 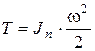), заменим сумму элементарных работ всех сил элементарной работой приведенного момента сил ( 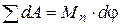) и разделим все на :

.

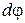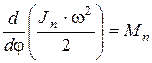Отсюда, взяв производную, получим

.

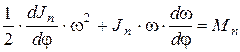Второе слагаемое левой части умножим и разделим на dt и сократим на 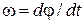. В результате получим уравнение движения в дифференциальной форме:

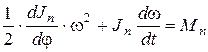. (6.20)

Здесь 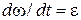– угловое ускорение начального звена.

При некоторых частных значениях функци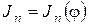й и 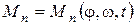, и при заданных начальных условиях 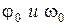законы движения определяются аналитически, т.е. уравнения (6.19) и (6.20) решаются, и можно найти зависимости 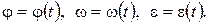Очевидно, что процесс решения будет наиболее простым, когда 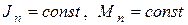. В общем случае уравнения (6.19) и (6.20) решают численными методами с помощью ЭВМ. Существуют также графоаналитические методы исследования движения, когда приведенный момент инерции 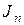и приведенный момент сил 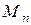зависят только от координаты .

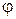Кроме определения истинного движения машины уравнения (6.19) и (6.20) позволяют провести качественный анализ движения, выявить общие закономерности. Пусть, например, для рычажного механизма (см. задания по контрольной работе №1) по результатам кинематического анализа определена зависимость .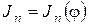

В заданиях к контрольной работе № 1 трением и внешним сопротивлением пренебрегаем, производственная нагрузка отсутствует, т.е. в формуле (6.18) 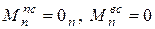. Кроме того, для механизма, рассматриваемого изолированно, приведенный момент сил двигателя 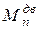следует заменить уравновешивающим моментом М_у, действующим на кривошип со стороны передаточного механизма, осуществляющего передачу движения от двигателя. Когда вал кривошипа соединен непосредственно с валом двигателя, то 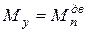. В этом случае из дифференциального уравнения движения (6.20) получим

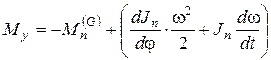, (6.21)

т.е., несмотря на отсутствие сопротивлений, момент М_у не равен нулю.

Даже если 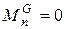(при горизонтальном движении звеньев) момент М_у не равен нулю для рычажных механизмов, в которых приведенный момент инерции 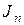в процессе движения изменяется: 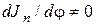. В этом случае при постоянной 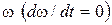, как принято в заданиях,

.

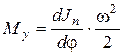С другой стороны, если идеальный механизм (без сопротивлений) предоставить самому себе (М_у=0), сообщив ему начальное движение, то при 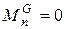из формулы (6.21) получим

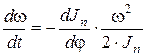, (6.22)

т.е. кривошип будет иметь угловое ускорение 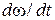в каждый момент времени пропорциональное быстроте изменения приведенного момента инерции 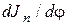. Дальнейшее решение уравнения (6.22) показывает, что в процессе движения изолированного, идеального механизма угловая скорость 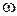изменяется обратно пропорционально 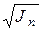. Следовательно, так же как и момент 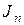, величина угловой скорости будет колебаться относительно некоторого среднего значения с периодом, равным времени одного оборота кривошипа.

Отметим еще, что если, в соответствии с принципом Даламбера, к действующим силам присоединить силы инерции звеньев, то для полученной уравновешенной системы сил можно записать

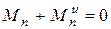, (6.23)

где 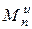- приведенный момент сил инерции звеньев.

Сравнивая уравнения (6.20) и (6.23), замечаем, что левая часть уравнения (6.20) численно равна приведенному моменту сил инерции, взятому со знаком минус.