Второго порядка первого вида

Определение реакций в кинематических парах в данном случае выполняется в такой последовательности.

1. Построение расчетной схемы. Группу Ассура в масштабе 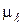изображают в заданном положении, рис.21. Прикладывают к звеньям группы все заданные внешние силы (силы тяжести G₂ и G₃) и силы инерции (главные векторы 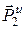, 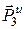и главные моменты 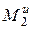, 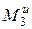сил инерции).

Рис. 21. Схема сил двуповодковой группы

2. Разложение неизвестных реакций во вращательных кинематических парах А и С на два направления: нормальное (параллельно звену) и тангенциальное (перпендикулярно зве­ну). В точке А будут приложены две составляющие: нормаль­ная реакция со стороны первого звена на второе 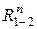и тангенциальная реакция со стороны первого звена на второе 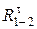. В точке В со стороны стойки на третье звено будут приложены нормальная реакция 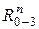и тангенциальная реакция 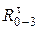. Направления векторов этих составляющих вначале задаются, а в дальнейшем уточняются.

Во время работы механизма на звенья действуют силы (или моменты) производственного сопротивления. В контрольной работе №1 рассматривается холостой ход, поэтому производственная нагрузка отсутствует.

3. Определение тангенциальных реакций в точках А и С. Тангенциальная реакция 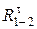определяется из условия ра­венства нулю суммы моментов сил, действующих на звено 2 (звено АВ) относительно точки В (рис. 21):

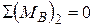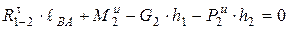, . (5.7)

Откуда

,

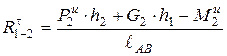где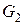 –вес звена 2.

Тангенциальная реакция 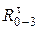определяется из условия равенства нулю суммы моментов сил, действующих на звено 3 (звено ВС) относительно точки В:

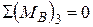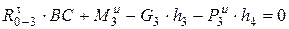, . (5.8)

Тогда

,

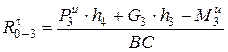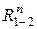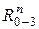4. Определение нормальных реакций в точках А и С. Нор­мальные реакции и определяются из условия равенства нулю геометрической суммы сил, действующих на группу звеньев 2 и 3. При записи этого векторного уравнения необходимо при­нять во внимание следующие условия:

а) запись векторного уравнения начинается с неиз­вестной составляющей реакции в точке A или C. Другая (известная) составляющая этой же реакции должна быть за­писана рядом;

б) силы, действующие на однозвено, не разделяются;

в) в конце векторного уравнения записывается вторая неиз­вестная составляющая.

Принимая во внимание эти рекомендации, составим век­торное уравнение для нашего случая:

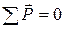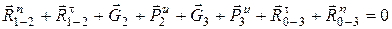, . (5.9)

На оснований векторного уравнения строится план сил в масштабе 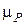(рис. 22). Из плана сил с помощью масштаба определяются неиз­вестные реакци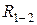и и .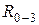

Для определения реакции со стороны третьего звена на второе 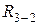необходимо воспользоваться условием равенст­ва нулю векторной суммы сил, действующих на звено 2:

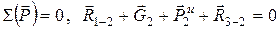. (5.10)

Реакция 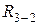определяется путем построения плана сил на основании последнего векторного уравнения. Однако построение этого плана не обязательно, поскольку реакцию 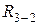можно определить по плану сил для

Рис. 22. План сил группы Ассура

группы звеньев 2 и 3 (рис. 22), соединив конец вектора 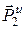, с началом вектора 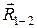. На рис. 22 реакция 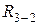обозна­чена штриховой линией.