Трение в кинематических парах. Коэффициент

Полезного действия

В относительном движении соприкасающихся под давлением элементовкинематическихпар между этими элементами возникает тре­ние, на преодоление которого затрачивается работа двигателя, приводящего в дви­жение механизм. При скольжении элементов кинематических пар сопротивление трения определяется силой трения скольжения 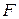, а при перекатывании – моментом трения качения .

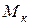В поступательной кинематической паре (рис. 23) полная реакция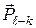, со стороны звена 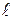на звено k отклоняется от нормали пп к плоскости касания элементов пары на угол трения 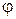в сторону, противоположную относительной скорости 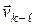звена k по отношению к звену 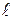. Угол трения равен

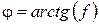, (5.11)

где 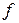– коэффициент трения скольжения.

Сила трения 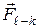, приложенная к звену k со стороны звена 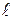, равна

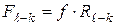, (5.12)

где 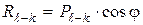– нормальная составляющая реакции 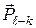. Очевидно, что при отсутствии трения реакция 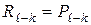. Равные, противоположно направленные силы приложены к звену 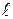со стороны звена .

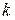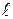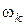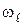Во вращательной кинематической паре (рис. 24) шип звена k и вкладыш подшипника звена вращаются с разными угловыми скоростями и соответственно. Вследствие разности угловых скоростей происходит относительное скольжение элементов пары, возникает сила трения скольжения (формула (5.12)):

,

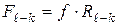где 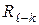– реакция в паре, определяемая при отсутствии трения. Показанная на рисунке сила приложена в точке контакта выполненных с зазором поверхностей шипа и отверстия вкладыша подшипника. Сила 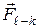создает относительно оси 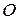шипа момент трения 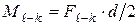, где d – диаметр шипа. При отсутствии трения момент 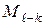будет равен нулю.

На преодоление сил трения в кинематических парах затрачивается часть мощности двигателя, приводящего в движение механизм. Эта мощность численно равна мощности, создаваемой силами трения. В поступательной паре модуль мощности сил трения (см. формулу (6.15)) равен

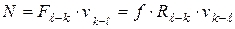. (5.13)

Величина скорости скольжения 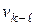определяется как модуль разности векторов скоростей точек соприкасающихся звеньев:

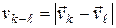. (5.14)

Если звено 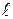неподвижно, то .

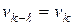Во вращательной паре модуль мощности сил трения вычисляется по формуле (6.16):

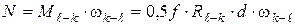, (5.15)

где 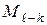– момент трения во вращательной паре; d – диаметр шипа, измеряемый в метрах; 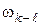– величина относительной угловой скорости звеньев, которая в плоских механизмах определяется как модуль разности алгебраических значений угловых скоростей звеньев:

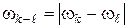. (5.16)

В частности, если звенья вращаются в разные стороны, то 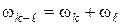. Угловые скорости 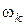, 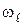и их направления определяются с помощью планов скоростей.

Мощность N_дв , развиваемая двигателем при работе механизма, идет на преодоление сил производственного сопротивления (полезная мощность) и на преодоление сил вредного сопротивления: трения в кинематических парах, а также сопротивления среды:

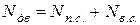, (5.17)

где 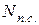– мощность, идущая на преодоление сил производственного сопротивления; 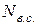– мощность, идущая на преодоление сил вредного сопротивления.

Эффективность использования энергии в данном механизме можно оценить отношением полезной мощности к мощности, затраченной двигателем при работе. Это отношение называют механическим коэффициентом полезного действия (к.п.д.):

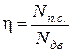. (5.18)

Чем больше 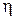, тем эффективнее работает машина.

В рычажных механизмах реакции в кинематических парах и скорости скольжения зависят от взаимного положения звеньев. Поэтому мощность 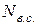, идущая на преодоление вредных сопротивлений, будет также меняться в течение одного цикла (одного оборота кривошипа). Следовательно, к.п.д. зависит от положения ведущего звена механизма и меняется от положения к положению. Чтобы оценить работу рычажного механизма, определяют мгновенные значения к.п.д. в нескольких положениях и вычисляют среднее значение.

В зубчатых механизмах значение к.п.д. за цикл меняется незначительно вследствие постоянства передаточного отношения, поэтому для подобных механизмов значение к.п.д. принимается неизменным, и его берут из справочников для различных видов зубчатых передач.

В случае сложного механизма, состоящего из нескольких более простых механизмов, соединенных последовательно, определить общий механический к.п.д. системы можно путем перемножения коэффициентов полезного действия составных простых механизмов. Таким образом находят общий к.п.д. сложных зубчатых передач:

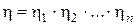, (5.19)

где 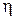– общий к.п.д. сложной зубчатой передачи; 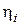– к.п.д. отдельной ступени (передачи); 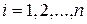– число отдельных ступеней (передач).