Силовой расчет кривошипно-ползунного механизма

Провести силовой расчет кривошипно-ползунного механизма компрессора (рис. 20, а) в положении, когда угол 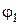= 45°. Размеры звеньев: 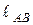= 100 мм, 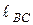= 400 мм. Нагрузка на звенья механизма: к звенуАВ в точке S₁ приложена сила Р₁=400 Н, она направлена вдоль линии АВ, рас­стояние 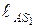= 20 мм; к звену 2 приложена сила Р₂=600 Н, она направлена под углом 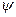= 60° к линии ВС и приложена в точке S₂. Расстояние 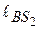= 100мм. К этому же звену приложен момент М₂ =8,0 нм; к звену 3 приложена сила Р₃ = 1000 Н, она направлена параллельно линии Ах и так, что ее линия действия проходит через точку С. Уравновешивающий момент M_у приложен к звену 1.

Подлежит определению: реакция R_0-3 в поступательной кинематичес­кой паре С, которая направлена перпендикулярно линии Ах; реакция R_2-3 во вра­щательной паре С; реакция R_1-2 во вращательной паре В; реакция R_0-1 во враща­тельной паре А и уравновешивающий момент M_у, приложенный к звену 1.

Замечание. Анализ плана ускорений на рис. 9, построенного для механизма в сходном положении, но с другими размерами звеньев, показывает, что силы, Р₁, Р₂, Р₃ и момент М₂ представляют собой инерционную нагрузку звеньев. По сравнению с заданием по контрольной работе №1 в данном примере для упрощения планов сил не учтены силы тяжести, которые следует добавить в уравнения равновесия. Однако при этом общий ход решения не изменяется.

Решение. 1. Все внешние силы, действующие на звенья механизма, заданы, поэтому данный этап выполнен.

2. Уравновешивающий момент My по условию приложен к звену1, поэтому ведущим звеном следует считать звено 1.

3. От механизма может быть отделена только одна группа Ассура, состоящая из звеньев 2 и 3. Эта группа относится ко второму классу второго порядка и второговида.

4. Составляем уравнения равновесия группы, состоящей из звеньев 2 и 3. Первоеиз уравнений (5.1) применительно к рассматриваемой группе запишется так:

.

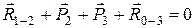В этом уравнении содержится три неизвестных: величина и направление реакции 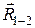и величина реакции 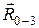. Для того чтобы его решить, т. е. чтобы построить представленную им векторную сумму, разложим реакцию 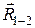на две составля­ющих: 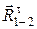,направленную перпендикулярно линии ВС, и 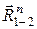направленную параллельно линии ВС. Теперь геометрическая сумма сил, приложенных к группе (рис. 20, б), равна

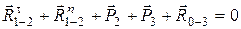. (5.3)

Величину силы 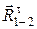найдем, рассматривая равновесие звена 2. Напишем ра­венство нулю суммы моментов относительно точки С всех сил, приложенных к зве­ну 2 (тем самым исключим из него момент неизвестной реакции 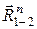), т. е. вкачестве второго уравнения (5.1) взято уравнение

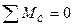, (5.4)

которое, будучи развернутым, примет вид

,

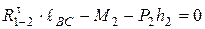откуда

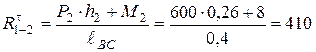Н,

где h₂ = 0,260 м найдено по чертежу. Строим план сил группы (рис. 20, в) по равенству (4.8) в масштабе 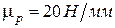. От точки а (рис. 20, в) отложим силу 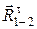в виде отрезка

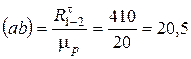мм.

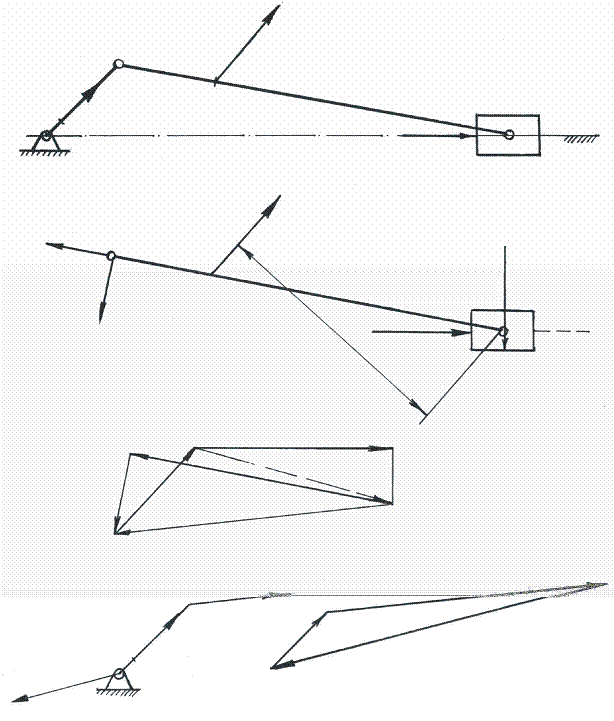Рис. 20. Силовой расчет кривошипно-ползунного механизма

От точки b откладываем силуР₂ в виде отрезка 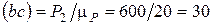мм, далее от точки с откладываем отрезок 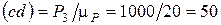мм, изображающий силу Р₃. Через точку а проводим прямую, параллельную ВС. Это будет линия действия силы 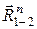,а через точку d – прямую, перпендикулярную Ах. Она будет линией действия силы 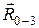. Находим точку пересечения е этих двух прямых. Отрезок (еа) в масштабе 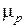дает искомую реакцию 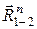, а отрезок (de) в том же масштабе – реакцию 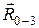, и, наконец, отрезок (be) дает искомую реакцию .

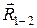Для нахождения реакции 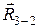напишем условие равновесия звена 2:

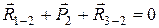. (5.5)

Из плана сил (рис. 20, в) видно, что отрезок (се) в масштабе 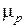соответствует иско­мой реакции 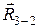. Реакция 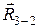должна проходить через точкуС, так как к ползуну 3 приложены только три силы, из которых две ( 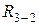и P₃) проходят через эту точку.

5. Силовой расчет ведущего звена 1 (рис. 20, г). К звену 1 приложены: сила Р₁ = 400 Н; сила 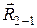= 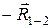(ее величина определяется из плана сил (рис. 20, в) отрезком (be), т.е. 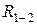= (be)· 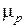= 1400 Н); сила (реакция) 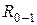и уравно­вешивающий момент M_у.

Из равенства нулю суммы моментов относительно точки A сил, приложенных к звену 1, находим величину момента уравновешивающей парысил:

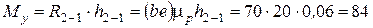Н·м,

где 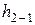– плечо силы 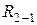, находится по чертежу (рис. 20, г). Условием равенства нулю векторной суммы сил, приложенных к звену1, будет

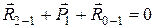. (5.6)

Отсюда находим модуль реакции 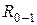путем построения векторного треугольника сил (рис. 20, д): 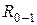= (ca)· 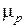(Н).