Силы инерции звеньев кривошипно-ползунного механизма

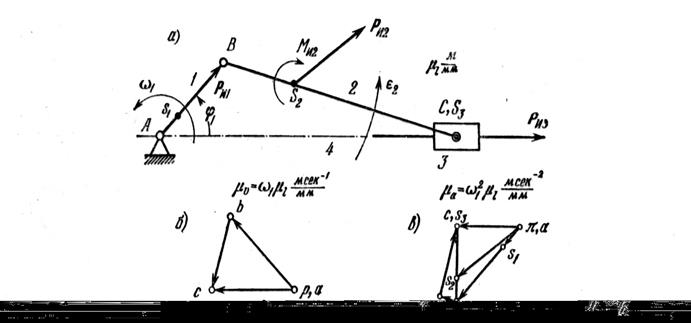
Для кривошипно-ползунного механизма (рис. 19) найти инер­ционную нагрузку всех звеньев. Заданы размеры звеньев 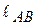, , 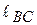, 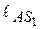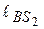; угловая скорость 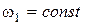; массы звеньев m₁, m₂, m₃; момент инерции 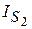. Решить для положения механизма, когда угол 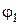= 45°.

Задаем масштаб чертежа 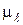и строим схему механизма (рис. 19, а). Выбрав длину отрезка (рb), изображающего скорость 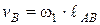точки В, вычислив масштаб 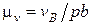, строим план скоростей в соответствии с уравнением

.

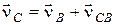Ускорение точки В равно 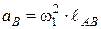. Задаваясь длиной отрезка ( 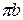), в масштабе 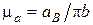строим план ускорений согласно формуле

.

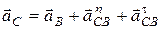Нормальное ускорение 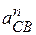точки С во вращательном движении звена ВС относительно точки В равно

,

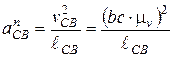где (bc) – отрезок, взятый с плана скоростей.

Рис. 19. Определение инерционной нагрузки звеньев кривошипно-ползунного механизма

Отрезок ( 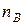), изображающий на плане ускорение 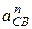точки С, найдется из равенства

.

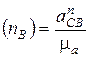По правилу подобия находим точки s₁, s₂, s₃ (концы векторов ускоренийцент­ров масс звеньев кривошипа АВ, шатуна ВС и ползуна 3). Подсчитываем инерционную нагрузку для каждого звена механизма.

Инерционные силы. Модули сил инерции звеньев определяются по формулам: 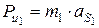, , 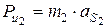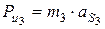. Векторы сил противоположны ускорениям центров масс. Величины ускорений определяются как произведения соответствующих отрезков плана ускорений ( 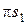, , 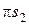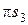) на масштаб 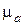плана.

Инерционные моменты. Для кривошипа АВ инерционный момент 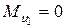, так как звено вращается равномерно. Для шатуна ВС модуль инерционного момента 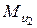,найдем по формуле (4.2):

.

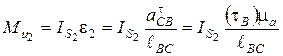Этот момент по направлению противоположен угловому ускорению звена ВС (рис. 19, а). Угловое ускорение звена ВС в нашем случае направлено против хода стрелки часов, в соответствии с направлением вектора 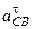тангенциального уско­рения точки С во вращении звена ВС относительно точки В. Для ползуна 3 инерционный момент 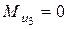, так как звено дви­жется поступательно.