Сложные зубчатые механизмы
В тех случаях, когда заданное передаточное отношение превышает целесообразное для одной пары колес или когда требуется обеспечить большое межосевое расстояние, используют сложные зубчатые механизмы. Различают сложные механизмы, представляющие собой последовательное соединение простых зубчатых передач с неподвижными осями колес, и планетарные зубчатые механизмы, в которых оси отдельных колес могут перемещаться относительно стойки. Сложные механизмы, в которых число подвижных звеньев с неподвижной осью вращения больше двух, называются многоступенчатыми. Каждая ступень осуществляет передачу движения от одного звена с неподвижной осью к следующему в кинематической цепи звену с неподвижной осью.
Общее передаточное отношение сложного многоступенчатого механизма, включающего несколько ступеней, в числе которых могут быть планетарные, равно произведению придаточных отношений отдельных ступеней.
Передача на рис. 12 включает пять подвижных звеньев и составлена из четырех непланетарных ступеней. Определим передаточное отношение от звена 1 к звену 5:
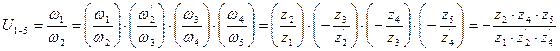
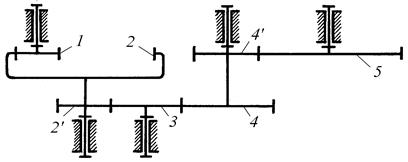
Рис. 12. Многоступенчатая передача с неподвижными осями колес
Анализ результата показывает, что, во-первых, при нечетном числе ступеней с внешним зацеплением колес общее передаточное отношение отрицательно, то есть колеса 1 и 5 будут вращаться в разные стороны. Во-вторых, число зубьев колеса 3, которое входит в зацепление сразу с двумя колесами 2 и 4, не влияет на величину передаточного отношения. Однако, если звено 3 убрать и ввести в зацепление колеса 2 и 4, общее передаточное отношение изменит знак. В данном механизме оно будет положительным, так как число ступеней с внешним зацеплением окажется четным. Такие колеса иногда называют паразитными. Они служат для изменения направления вращения выходного колеса или для увеличения расстояния между осями входного и выходного колес.
В технике часто используют так называемые коробки скоростей (передач) (рис. 13), которые позволяют скачкообразно изменять скорость вращения выходного звена при неизменной скорости входного звена. Колеса 1, 2 и 3 образуют единый блок, который может перемещаться вдоль вала 1 на скользящей шпонке и сцепляться либо с колесом 4, либо с колесом 5, либо с колесом 6.
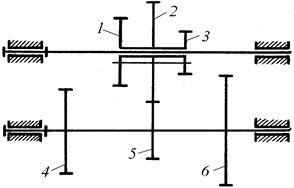
Рис. 13. Коробка скоростей
В такой конструкции должно выполнятся условие соосности:
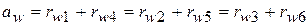
где 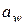 - межосевое расстояние;
- межосевое расстояние; 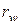 - радиусы начальных окружностей колес.
- радиусы начальных окружностей колес.
Если колеса не корригированные и имеют одинаковый модуль, условие принимает вид:
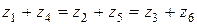
Планетарные механизмы
Колеса планетарных механизмов, геометрические оси которых неподвижны и совпадают с центральной осью передачи, называются центральными или солнечными колесами. На рис. 14 колеса 1 и 3. Зубчатые колеса, оси которых подвижны (колесо 2, рис. 14), называются сателлитами. Звено, на котором располагаются подвижные оси сателлитов, называется водилом и обозначается буквой Н. Центральные колеса 1 и 3 и водило Н, оси вращения которых совпадают с центральной осью передачи, называются основными звеньями.
Определим степень подвижности механизма на рис.14. Механизм имеет четыре подвижных звена, четыре кинематические пары пятого класса и две пары четвертого класса. Тогда по формуле Чебышева
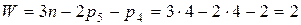 .
.
Планетарные механизмы, у которых степень подвижности равна двум, называются дифференциальными или просто дифференциалами. Чтобы получить определенное движение всех звеньев дифференциала, двум из них надо задать независимые движения. Например, входными звеньями можно сделать центральные колеса 1 и 3, тогда выходным звеном будет являться водило Н. Если одно из центральных колес, 1 или 3, жестко соединить со стойкой (закрепить), то степень подвижности механизма будет равна единице. Такой механизм называется планетарным эпициклическим или просто планетарным. Планетарными являются, например, механизмы на рис. 15 а, б.
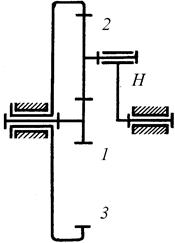
Рис. 14. Дифференциальный зубчатый механизм
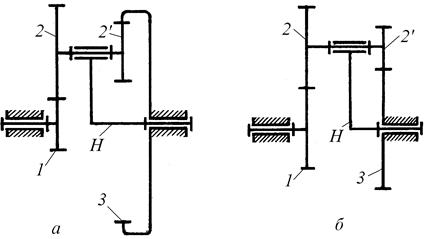
Рис. 15. Планетарные передачи
Соотношение между угловыми скоростями звеньев любых планетарных передач устанавливается с помощью метода обращения движения. Метод заключается в том, что всем звеньям механизма, включая стойку, условно сообщается дополнительная угловая скорость, равная по величине угловой скорости водила, но направленная в противоположную сторону ( 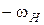 ). При этом водило превращается в стойку, а стойка получает вращение вокруг центральной оси со скоростью «
). При этом водило превращается в стойку, а стойка получает вращение вокруг центральной оси со скоростью « 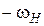 ».
».
В обращенном механизме передаточное отношение от некоторого звена к к звену 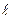 равно
равно
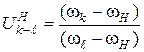 , (3.8)
, (3.8)
где 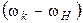 и
и 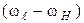 – новые угловые скорости звеньев к и
– новые угловые скорости звеньев к и 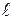 в обращенном движении.
в обращенном движении.
Верхний индекс в обозначениях передаточных отношений указывает,
какое звено остановлено. Формула (3.8) называется формулой Виллиса. Удобство ее заключается в том, что в обращенном механизме оси всех колес неподвижны, поэтому передаточное отношение 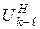 можно выразить через числа зубьев. Например, в механизме на рис. 14 для колес 1 и 3
можно выразить через числа зубьев. Например, в механизме на рис. 14 для колес 1 и 3
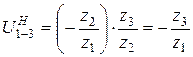 .
.
Подставив в формулу (3.8), получим
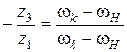 .
.
Здесь  – угловые скорости звеньев в реальном (не обращенном) механизме. Задавая значения двух из них, можно определить значение третьей.
– угловые скорости звеньев в реальном (не обращенном) механизме. Задавая значения двух из них, можно определить значение третьей.
Для планетарного механизма с неподвижным колесом 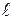 (
( 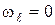 ), формула Виллиса (3.8) принимает вид
), формула Виллиса (3.8) принимает вид
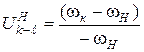 или
или 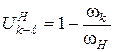 .
.
Учитывая, что 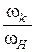 – это передаточное отношение от колеса к к водилу Н при неподвижном колесе
– это передаточное отношение от колеса к к водилу Н при неподвижном колесе 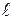 получим
получим
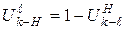 . (3.9)
. (3.9)
Передаточное отношение в реальном механизме равно единице минус передаточное отношение в обращенном механизме.
В механизме на рис. 15, а неподвижно колесо 3, тогда по формуле (3.9)
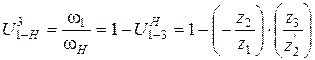 .
.
Для механизма на рис. 15, б
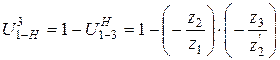
Формула (3.9) позволяет получить передаточное отношение от колеса к к водилу H. Если требуется вычислить передаточное отношение от водила к колесу к при неподвижном колесе 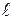 , формулу следует преобразовать. Учитывая, что
, формулу следует преобразовать. Учитывая, что
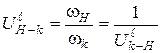 ,
,
с помощью формулы (3.9) получим
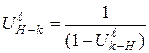 . (3.10)
. (3.10)
В механизме на рис. 15, б передаточное отношение от водила к колесу 1 равно
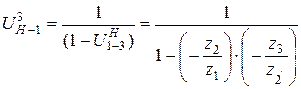 .
.
При определении передаточного отношения сложного механизма важно правильно разделить его на ступени, особенно когда в механизме имеются планетарные ступени. Планетарная ступень всегда начинается с основного звена, то есть звена, ось вращения которого неподвижна относительно стойки, и заканчивается ближайшим основным звеном, с которого вращение передается на следующую ступень механизма. Например, в комбинированном механизме на рис. 16 две планетарные ступени. Первая начинается с колеса 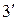 включает в себя колеса 4 и 5 и заканчивается водилом H1, вторая начинается с водила Н2, заканчивается колесом 10. Общее передаточное отношение от колеса 1 к колесу 10 равно
включает в себя колеса 4 и 5 и заканчивается водилом H1, вторая начинается с водила Н2, заканчивается колесом 10. Общее передаточное отношение от колеса 1 к колесу 10 равно
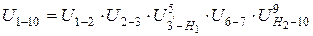
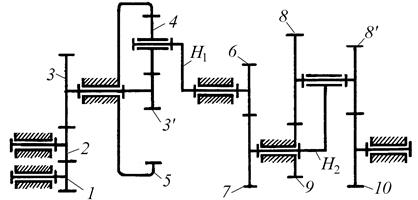
Рис. 16. Комбинированный зубчатый механизм
Выразив передаточные отношения в первой части равенства через числа зубьев колес, после преобразования получим
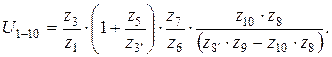
Часть вторая. Динамика механизмов и машин
Дата добавления: 2021-12-14; просмотров: 552;











