КИНЕМАТИЧЕСКОЕ ИССЛЕДОВАНИЕ ПЛОСКИХ РЫЧАЖНЫХ МЕХАНИЗМОВ

2.1. Построение положений механизма и

траекторий точек звеньев

Кинематическое исследование механизма графическим методом начинается с по­строения ряда положений механизма, соответствующих одно­му циклу его работы. Положения механизма иначе называ­ются планами механизма. Построение положений механизма (или планов) произво­дится в масштабе, соответствующем стандартному линейному масштабу.

Часто за исходное (нулевое) положение механизма принимают одно из его двух крайних положений. В контрольной работе №1 это условие не устанавливается, исходным принято положение, в котором кривошип расположен вертикально.

Крайним называется такое поло­жение механизма, в котором абсолютная скорость точек выходного звена равна нулю. В качестве примера рассмотрим построение положений (в том числе и крайних) кривошипно-коромыслового механиз­ма (рис. 4).

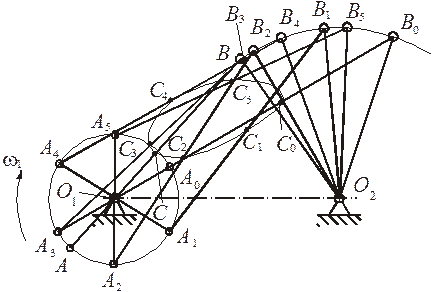Рис. 4. Планы положений механизма

Крайние положения кривошипно-коромыслового механиз­ма соответствуют расположению кривошипа и шатуна на од­ной прямой линии. Положение точек В₀ и В в этих положениях определяется за­сечками, сделанными из центра О₁ радиусами, равными О₁A+АВ и АВ–О₁А, на дуге радиуса О₂В. Примем за исходное крайнее правое положение. Рассматриваемые положения ме­ханизма строятся через равные промежутки времени. На рис. 4 приведено построение шести положении механизма. Положения кривошипа О₁А определяются делением окруж­ности радиуса О₁А на 6 равных частей. Положения шатуна АВ и коромысла O₂В определяются графически, путем засечек радиусом АВ из точек А на дуге радиуса O₂В, проведенной из точки О₂.

Траектория какой-либо точки звена механизма строится путем последовательного соединения плавной линией поло­жений этой точки, соответствующих положениям механизма. На рис. 4 изображена траектория точки С шатуна – так называемая шатунная кривая.

Скорости и ускорения точек звеньев

В плоском движении

Рассмотрим векторные уравнения и формулы, лежащие в основе построения планов скоростей и ускорений для всех видов плоского движения звеньев, встречающихся в механиз­мах машин: вращательного, поступательного и плоскопараллельного.

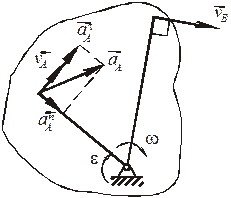
Вращательное движение. Звено ОА, рис. 5, совершает вращательное движение вокруг неподвижного центра О. Кинематическое состояние звена в каждый дан­ный момент времени вполне определяется значением его угловой скорости 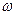и углового ускорения 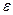. Окружные скорость точек перпендикулярны радиусам. Их модули равны

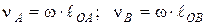. (2.1)

Ускорениелюбой точки определится как векторная сумма нормального и тангенциального ускорений:

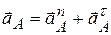, (2.2)

модули которых определяются по формулам

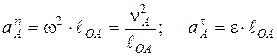. (2.3)

Поступательное движение. При поступательном движении все точки тела описывают одинаковые траектории и в каждый любой момент времени имеют одинако­вые по величине и направлению скорости и ускорения. Для изучения поступательного движения твердого тела достаточно определить тра­екторию, скорость и ускорение одной его точки.

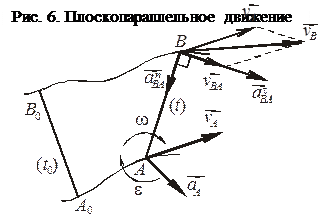
Плоскопараллельное движение.Из теоретической механики известно, что плоско­параллельное движение звена в любом положении может быть составлено из мгновенного поступательного движения со скоростью, равной скорости произвольно выбранной точки звена (полюса), и мгновенного вращательного движения вокруг полюса.

Таким образом, ско­рость любой точки звена может быть определена как геомет­рическая сумма вектора скорости полюса и вектора скорости этой точки во вращательном движении звена вокруг полюса.

Если за полюс принять точку А (рис. 6), то в момент времени t скорость точ­ки В звена АВ может быть выражена следующим образом:

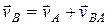, (2.4)

где 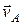– скорость точки А; 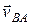– скорость точки В относительно точки А.

Вектор скорости 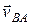направлен перпендикулярно звену АВ в сторону, определяемую направлением угловой скорости этого звена. Величина скорости 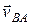равна

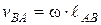, (2.5)

здесь 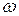– угловая скорость звена АВ; 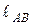– длина звена АВ.

Ускорение любой точки звена также может быть выра­жено как геометрическая сумма векторов ускорения полюса и вектора ускорения точки во вращательном движении звена вокруг полюса.

Вектор ускорения точки В (рис. 6) равен:

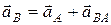, (2.6)

где 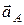– ускорение точки А; 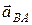– ускорение точки В от­носительно точки А.

Вектор ускорения 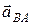может быть разложен на нормаль­ное и тангенциальное ускорения:

.

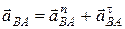Здесь 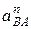– нормальное ускорение точки В при ее движе­нии относительно точки А; 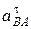– тангенциальное ускорение точки В при ее дви­жении относительно точки А.

Тогда

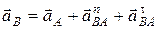. (2.7)

Модуль нормального ускорения точки В относи­тельно точки А равен:

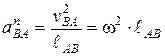. (2.8)

Ускорение 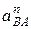направлено по оси звена АВ от точки В к точке А. Величина тангенциального ускорения точки В относительно точки А равна

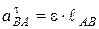, (2.9)

где 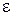- угловое ускорение звенаАВ.

Вектор ускорения 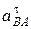направлен перпендикулярно звену АВ в сторону, определяемую направлением углового ускоре­ния .

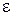2.3. Построение планов скоростей и ускорений